Ecuaciones de la dinámica del sólido rígido

De Laplace

1 Introducción

Un sólido, como cualquier otro sistema de partículas está sometido a un conjunto de fuerzas. Las fuerzas sobre cada partícula pueden ser internas (debidas a otra partícula del mismo sólido) o externas (debidas a un agente externo, como la gravedad o un campo eléctrico aplicado).

Las fuerzas internas son importantes en cuanto a que son las que producen la propia existencia del sólido. Se trata de fuerzas cohesivas intensas que consiguen que cada átomo mantenga una posición aproximadamente fija respecto al resto de partículas del sólido.

Sin embargo, una vez admitida la aplicabilidad del modelo de sólido rígido, podemos ignorar la presencia de las fuerzas internas.

La razón es la siguiente: el movimiento de un sólido rígido posee 6 grados, que se pueden describir mediante las tres componentes de la velocidad lineal de un punto y las tres componentes de la velocidad angular del sólido. A su vez, estos dos vectores se relacionan directamente con la cantidad de movimiento y el momento cinético del sólido.

Por tanto, para determinar las ecuaciones de movimiento del sólido nos basta con el teorema de la cantidad de movimiento y el teorema del momento cinético. Para un sistema de partículas cualquiera (entre los que se incluye el sólido rígido), las ecuaciones de evolución de 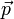y dependen exclusivamente de las fuerzas externas aplicadas sobre el sistema, por lo que podemos restringirnos a ellas.

Suponemos entonces que sobre la partícula m_i de un sólido actúa la fuerza externa 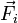. Estas fuerzas pueden ser debidas a que algún agente externo actúa sobre ellas o pueden ser fuerzas de reacción vincular (o una combinación de ambas). Así, en una articulación entre dos sólidos, cada uno de ellos experimenta un conjunto de fuerzas de reacción vincular que los obligan a moverse como corresponde al par cinemático correspondiente y no de otra forma.

2 Campo de velocidades del sólido

Según el teorema de Chasles, la velocidad de cualquier punto de un sólido puede hallarse conocida la velocidad de un punto de referencia, A, y la velocidad angular del sólido

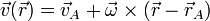
En particular, el punto de referencia puede ser el centro de masas del sólido

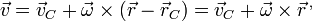
3 Movimiento del centro de masas

Para determinar el movimiento del centro de masas nos basta con aplicar que para un sistema de partículas

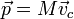
y, derivando aquí respecto al tiempo,

siendo la resultante de todas las fuerzas aplicadas sobre el sólido, independientemente de sobre qué partícula se apliquen.

Según esto, basta con sumar vectorialmente las diferentes fuerzas aplicadas para determinar la aceleración del CM, el cual se moverá como una partícula cuya masa sea la total del sólido.

En el caso particular del peso, la resultante es

Es decir, la resultante del peso de todo el sólido equivale al peso de una sola partícula cuya masa sea la total del sólido. Esta ecuación, junto con la anterior, nos dice que si un objeto es lanzado y se encuentra sometido exclusivamente a su peso, su centro de masas describe una parábola.

Este resultado no quiere decir que el sólido se traslade con la velocidad del CM, sino que, n general, el sólido describirá un movimiento de rotación en torno al centro de masas. Para determinar la evolución de la velocidad angular con la que rota debemos recurrir a la ecuación para el momento cinético.

4 Movimiento alrededor del centro de masas

El momento cinético de un sólido respecto a un punto O equivale a, de acuerdo con las propiedades de un sistema de partículas,

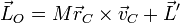
con 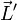el momento cinético correspondiente al movimiento respecto al CM. En el caso de un sólido simétrico respecto al eje de giro, esta expresión se reduce a

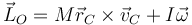
por ello, su derivada respecto al tiempo nos da la ecuación de movimiento para la rotación del sólido.

La derivada respecto al tiempo de esta cantidad es

Asimismo, esta derivada equivale a la resultante de los momentos de las fuerzas aplicadas sobre las distintas partículas del sólido

Separando los vectores de posición

el momento resultante se puede descomponer en

Igualando las dos expresiones nos queda

Por tanto, para determinar la rotación del sólido en torno al CM nos basta con calcular la resultante de las momentos respecto al CM de las diferentes fuerzas aplicadas sobre el sólido.

En el caso de un sólido simétrico, esta derivada temporal es igual a

A diferencia de la ecuación de la cantidad de movimiento, en la que la masa es una constante, el momento de inercia, aunque se trate de un sólido simétrico es una función del tiempo. La razón es que el eje respecto al que se calcula puede estar cambiando en el tiempo, por lo que en cada instante I va a representar una magnitud diferente.

No obstante, el momento de inercia es constante en los siguientes casos particulares de interés:

• Rotación en torno a un eje fijo (p.ej. un rotor, o un péndulo que oscila en torno a un anclaje fijo).
• La dirección de la velocidad angular es constante (como ocurre en el movimiento plano).
• El momento de inercia es independiente del eje que se elija, siempre que pase por el CM del sólido (p.ej., para una esfera, pero también para un sólido cúbico).

En esos casos, la ecuación se reduce a

con α la aceleración angular. Esta ecuación es el análogo para rotación de la segunda ley de Newton.

5 Sistemas equivalentes