Ecuaciones de la dinámica del sólido rígido
De Laplace
Contenido |
1 Introducción
Un sólido, como cualquier otro sistema de partículas está sometido a un conjunto de fuerzas. Las fuerzas sobre cada partícula pueden ser internas (debidas a otra partícula del mismo sólido) o externas (debidas a un agente externo, como la gravedad o un campo eléctrico aplicado).
Las fuerzas internas son importantes en cuanto a que son las que producen la propia existencia del sólido. Se trata de fuerzas cohesivas intensas que consiguen que cada átomo mantenga una posición aproximadamente fija respecto al resto de partículas del sólido.
Sin embargo, una vez admitida la aplicabilidad del modelo de sólido rígido, podemos ignorar la presencia de las fuerzas internas.
La razón es la siguiente: el movimiento de un sólido rígido posee 6 grados, que se pueden describir mediante las tres componentes de la velocidad lineal de un punto y las tres componentes de la velocidad angular del sólido. A su vez, estos dos vectores se relacionan directamente con la cantidad de movimiento y el momento cinético del sólido.
Por tanto, para determinar las ecuaciones de movimiento del sólido nos basta con el teorema de la cantidad de movimiento y el teorema del momento cinético. Para un sistema de partículas cualquiera (entre los que se incluye el sólido rígido), las ecuaciones de evolución de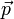 
y 
dependen exclusivamente de las fuerzas externas aplicadas sobre el sistema, por lo que podemos restringirnos a ellas.
