Partícula en tubo que gira (sistema no inercial) (G.I.A.)

De Laplace

Revisión a fecha de 12:10 28 dic 2011; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Una partícula de masa

m

se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme

ω

en torno a un eje perpendicular al del tubo. Obtenga las ecuaciones de movimiento para la partícula aplicando los resultados del movimiento relativo de sólidos rígidos.

2 Solución

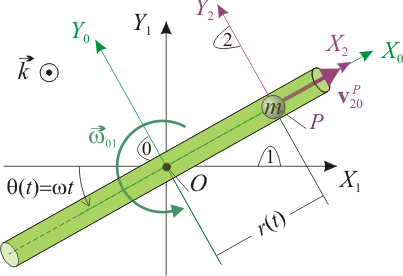
El análisis del sistema bajo estudio puede realizarse en términos del movimiento relativo de sólidos rígidos: el plano horizontal fijo, y el tubo no deformable que, siempre contenido en dicho plano, gira con velocidad angular constante $ω$ alrededor de un eje vertical que pasa por un punto $O$ del tubo.

2.1 Identificación y caracterización de movimientos relativos

Comos sabemos, sólido rígido y sistema de referencia son conceptos equivalentes. Así, podemos identificar el sólido “1” (plano fijo) con un sistema de referencia $O X 1 Y 1 Z 1$ cuyo plano $O X 1 Y 1$ coincida geométricamente con aquél, y de manera que el tubo gire en torno al eje $O Z 1$ . Por su parte, el tubo (sólido “0”) se moverá solidariamente con un sistema de referencia $O X 0 Y 0 Z 0$ cuyo origen va a estar en el punto por el que pasa el eje de rotación y que, por tanto, va a estar en reposo permanente respecto del sistema de referencia fijo. Además, para simplificar la descripción tomaremos el eje $O Z 0$ en la dirección vertical al plano de movimiento (es decir, coincidiendo con el $O Z 1$ ), y el $O X 0$ en la dirección longitudinal del tubo. De esta forma, la reducción cinemática (y su derivada) que permite describir el movimiento instantáneo del sólido “0” (tubo delgado) respecto del sólido “1” (plano fijo), es:

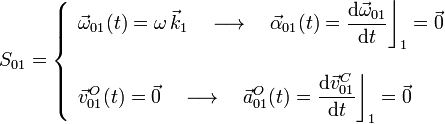
$S_{01}=\left\{\begin{array}{l}\displaystyle\vec{\omega}_{01}(t)=\omega\!\ \vec{k}_1\quad\longrightarrow\quad\vec{\alpha}_{01}(t)=\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}\\ \\ \displaystyle\vec{v}_{01}^O(t)=\vec{0}\quad\longrightarrow\quad\vec{a}_{01}^O(t)=\frac{\mathrm{d}\vec{v}_{01}^C}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}\end{array}\right.$

Pero el objeto de estudio es la partícula $P$ que puede recorrer sin rozamiento el interior del tubo. Para describir las propiedades geométricas del movimiento de este punto material podemos seguir utilizando el formalismo de la cinemática del movimiento relativo de sólidos si consideramos que dicha partícula forma parte de un tercer sólido rígido (sólido “2”). La elección de las direcciones del sistema de referencia asociado, $P X 2 Y 2 Z 2$ , y como se mueva este triedro respecto de los otros sólidos va a ser completamente irrelevante. Sólo es importante que tomemos el punto $P$ como centro de reducción. Así, optaremos por un sistema de referencia-sólido “2” que realice un movimiento simple: por ejemplo, un movimiento de traslación permanente, de manera que todos los puntos de dicho sólido se desplacen siempre paralelos al punto $P$ . Y como dicho punto se desplaza siempre por el interior el tubo, o lo que es lo mismo, a lo largo del eje $O X 0$ , la reducción cinemática del movimiento relativo del sólido “2” respecto del sólido “0”, es:

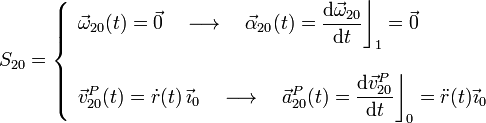
$S_{20}=\left\{\begin{array}{l}\displaystyle\vec{\omega}_{20}(t)=\vec{0}\quad\longrightarrow\quad\vec{\alpha}_{20}(t)=\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}\\ \\ \displaystyle\vec{v}_{20}^P(t)=\dot{r}(t)\!\ \vec{\imath}_0\quad\longrightarrow\quad\vec{a}_{20}^P(t)=\frac{\mathrm{d}\vec{v}_{20}^P}{\mathrm{d}t}\bigg\rfloor_0=\ddot{r} (t)\vec{\imath}_0\end{array}\right.$

donde $r (t)$ es la distancia desde la partícula hasta el punto fijo $O$ , de manera que...

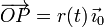
$\overrightarrow{OP}=r(t)\!\ \vec{\imath}_0$

La reducción cinemática del movimiento {21} lo obtemos por composición de los movimientos {20} y {01}:

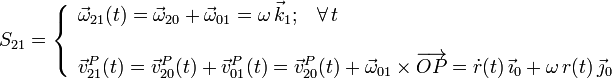
$S_{21}=\left\{\begin{array}{l}\displaystyle\vec{\omega}_{21}(t)=\vec{\omega}_{20}+\vec{\omega}_{01}=\omega\!\ \vec{k}_1\mathrm{;}\quad\forall\, t\\ \\ \displaystyle\vec{v}_{21}^P(t)=\vec{v}_{20}^P(t)+\vec{v}_{01}^P(t)=\vec{v}_{20}^P(t)+\vec{\omega}_{01}\times\overrightarrow{OP}=\dot{r}(t)\!\ \vec{\imath}_0+\omega\!\ r(t)\!\ \vec{\jmath}_0\end{array}\right.$

Los valores instantáneos de las derivadas temporales de los elementos de esta reducción se obtienen también por composición de movimientos:

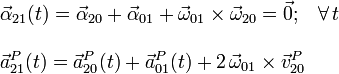
$\begin{array}{l}\displaystyle\vec{\alpha}_{21}(t)=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}\times\vec{\omega}_{20}=\vec{0}\mathrm{;}\quad\forall\, t\\ \\ \displaystyle\vec{a}_{21}^P(t)=\vec{a}_{20}^P(t)+\vec{a}_{01}^P(t)+2\!\ \vec{\omega}_{01}\times\vec{v}_{20}^P\end{array}$

donde falta por calcular la aceleración “de arrastre“ (movimiento {01}) del punto $P$ :

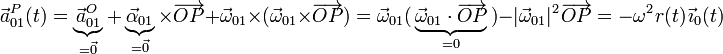
$\vec{a}_{01}^P(t)=\underbrace{\vec{a}_{01}^O}_{=\vec{0}}+\underbrace{\vec{\alpha}_{01}}_{=\vec{0}}\times\overrightarrow{OP}+\vec{\omega}_{01}\times\big(\vec{\omega}_{01}\times\overrightarrow{OP}\big)=\vec{\omega}_{01}\big(\underbrace{\vec{\omega}_{01}\cdot\overrightarrow{OP}}_{=0}\big)-|\vec{\omega}_{01}|^2\!\ \overrightarrow{OP}=-\omega^2\!\ r(t)\!\ \vec{\imath}_0(t)$

Sustituyendo y operando en la expresión de la aceleración instantánea “absoluta” se obtiene:

$\vec{a}_{21}^P(t)=\bigg[\ddot{r}(t)-\omega^2\!\ r(t)\bigg]\!\ \!\ \vec{\imath}_0(t)+2\omega\dot{r}(t)\!\ \vec{\jmath}_0(t)$

Partícula en tubo que gira (sistema no inercial) (G.I.A.)

De Laplace

1 Enunciado

2 Solución

2.1 Identificación y caracterización de movimientos relativos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES