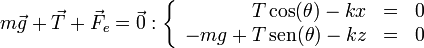Partícula suspendida de resorte y barra
De Laplace
Contenido |
1 Enunciado
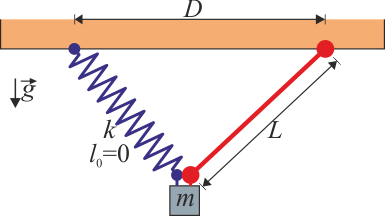
Una partícula de peso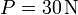 
se encuentra atada simultáneamente a una barra rígida de longitud 
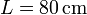y a un muelle de longitud natural nula y constante 
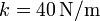. Los anclajes de la barra y el resorte distan 
.
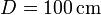- Determine la posición de equilibrio de la masa. ¿Cuánto vale la tensión de la barra en este momento? ¿Cuál es la longitud del resorte?
- Suponga que se corta la unión de la masa con el resorte. ¿Qué tipo de movimiento describe la masa a partir de ese momento? Halle la rapidez máxima que alcanza.
- Suponga que, en lugar de lo anterior, se corta la unión de la masa con la barra. ¿Qué movimiento describe en ese caso? Calcule la amplitud y frecuencia del movimiento resultante. Halle la rapidez máxima que alcanza.
2 Posición de equilibrio
Según sea de grande la masa de la partícula, el resorte se estirará más o menos. La posición de equilibrio será aquella en que la suma de fuerzas sea igual a cero.
Sobre la masa actúan tres fuerzas: el peso, la tensión de la barra y la fuerza recuperadora del muelle, por lo que
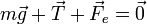
Si consideramos el origen de coordenadas en el punto de anclaje del resorte, y el eje Z como el vertical hacia arriba, el peso tiene la expresión en la base cartesiana
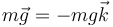
La fuerza recuperadora vale, puesto que la longitud en reposo del resorte es nula,
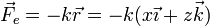
La tensión tiene módulo T y va en la dirección de la barra. Si ésta forma un ángulo θ con la horizontal
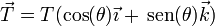
Llevando todo esto a la ecuación de equilibrio nos quedan las ecuaciones
