Partícula suspendida de resorte y barra

De Laplace

1 Enunciado

Una partícula de peso 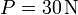se encuentra atada simultáneamente a una barra rígida de longitud 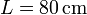y a un muelle de longitud natural nula y constante 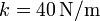. Los anclajes de la barra y el resorte distan .

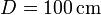1. Determine la posición de equilibrio de la masa. ¿Cuánto vale la tensión de la barra en este momento? ¿Cuál es la longitud del resorte?
2. Suponga que se corta la unión de la masa con el resorte. ¿Qué tipo de movimiento describe la masa a partir de ese momento? Halle la rapidez máxima que alcanza.
3. Suponga que, en lugar de lo anterior, se corta la unión de la masa con la barra. ¿Qué movimiento describe en ese caso? Calcule la amplitud y frecuencia del movimiento resultante. Halle la rapidez máxima que alcanza.

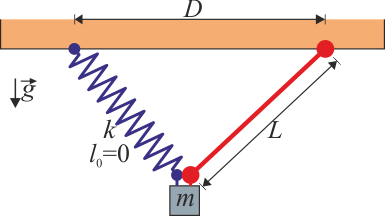
2 Posición de equilibrio

Según sea de grande la masa de la partícula, el resorte se estirará más o menos. La posición de equilibrio será aquella en que la suma de fuerzas sea igual a cero.

Sobre la masa actúan tres fuerzas: el peso, la tensión de la barra y la fuerza recuperadora del muelle, por lo que

\

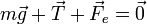
3 Partícula sujeta a la barra

4 Partícula sujeta al resorte