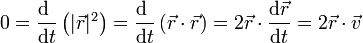Entrar Página Discusión Historial Go to the site toolbox

Conservación en un oscilador armónico tridimensional

De Laplace

Contenido

1 Enunciado

Una partícula de masa 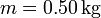m=0.50\,\mathrm{kg} se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke

\vec{F}=-k\vec{r}\qquad\qquad k = 2.00\,\mathrm{N}/\mathrm{m}

siendo su posición y velocidad iniciales

\vec{r}_0 = (-12.0\,\vec{\imath}+11.0\vec{\jmath})\,\mathrm{m}\qquad \qquad \vec{v}_0=(-8.0\vec{\imath}+24.0\,\vec{\jmath})\,\frac{\mathrm{m}}{\mathrm{s}}
  1. Calcule el momento cinético de la partícula respecto al origen de coordenadas
  2. Halle la energía mecánica de la partícula
  3. Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza

2 Momento cinético

El momento cinético de la partícula es una constante de movimiento, por tratarse de una fuerza central. Su valor lo obtenemos a partir de la posición y la velocidad iniciales

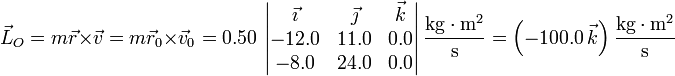
\vec{L}_O=m\vec{r}\times\vec{v} = m\vec{r}_0\times\vec{v}_0 = 0.50\,\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -12.0 & 11.0 & 0.0 \\ -8.0 & 24.0 & 0.0\end{matrix}\right|\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}=\left(-100.0\,\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}

3 Energía mecánica

La energía mecánica es suma de la cinética más la potencial.

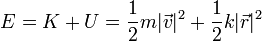
E = K + U = \frac{1}{2}m|\vec{v}|^2+\frac{1}{2}k|\vec{r}|^2

Esta cantidad también es constante, por tratarse de una fuerza conservativa. Su valor lo obtenemos de nuevo a partir de las condiciones iniciales.

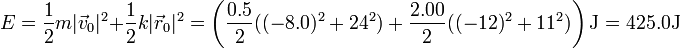
E = \frac{1}{2}m|\vec{v}_0|^2+\frac{1}{2}k|\vec{r}_0|^2 = \left(\frac{0.5}{2}((-8.0)^2+24^2)+\frac{2.00}{2}((-12)^2+11^2)\right)\mathrm{J}=425.0\mathrm{J}

4 Distancias y velocidades extremas

En su movimiento, la partícula describe una elipse, alcanzando una distancia máxima y una m´´inima respecto al centro (lo que se denominan semieje mayor y menor de la elipse). Para hallar esta distancia no nos basta con la ley de conservación de la energía, pues tenemos dos incógnitas para cada punto: la posición y la rapidez. La segunda ecuación la obtenemos de la conservación del momento cinético.

En un punto de distancia máxima (o mínima) al origen la velocidad es perpendicular al vector de posición. Para verlo consideramos que si la distancia es máxima, su derivada es nula, por lo que

0 = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(|\vec{r}|^2\right) =\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\vec{r}\cdot\vec{r}\right) = 2\vec{r}\cdot\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=2\vec{r}\cdot\vec{v}
Obtenido de "http://tesla.us.es/wiki/index.php/Conservaci%C3%B3n_en_un_oscilador_arm%C3%B3nico_tridimensional"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace