Entrar Página Discusión Historial Go to the site toolbox

Conservación en un oscilador armónico tridimensional

De Laplace

Revisión a fecha de 14:47 4 dic 2011; Antonio (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado

Una partícula de masa 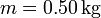m=0.50\,\mathrm{kg} se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke

\vec{F}=-k\vec{r}\qquad\qquad k = 2.00\,\mathrm{N}/\mathrm{m}

siendo su posición y velocidad iniciales

\vec{r}_0 = (-12.0\,\vec{\imath}+11.0\vec{\jmath})\,\mathrm{m}\qquad \qquad \vec{v}_0=(-8.0\vec{\imath}+24.0\,\vec{\jmath})\,\frac{\mathrm{m}}{\mathrm{s}}
  1. Calcule el momento cinético de la partícula respecto al origen de coordenadas
  2. Halle la energía mecánica de la partícula
  3. Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza

2 Momento cinético

3 Energía mecánica

4 Distancias y velocidades extremas

Obtenido de "http://tesla.us.es/wiki/index.php/Conservaci%C3%B3n_en_un_oscilador_arm%C3%B3nico_tridimensional"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace