Cuestión de equilibrio estático, Noviembre 2011

De Laplace

Revisión a fecha de 10:20 25 nov 2011; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

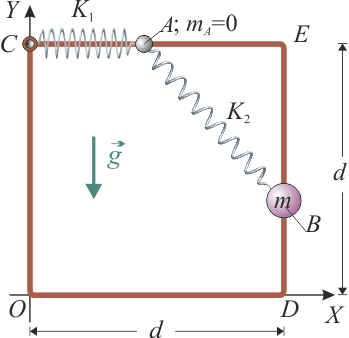
Cuatro varillas de igual longitud

d

están dispuestas formando un cuadrado

O D E C

, contenido en el plano vertical

O X Y

. Un resorte de longitud natural nula y constante recuperadora

K 1

conecta el vértice fijo

C

del cuadrilátero con un punto

A

de masa despreciable que puede desplazarse a lo largo de la varilla horizontal superior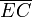 $\overline{EC}$ . Además, una partícula material

B

, cuya masa tiene un valor

m

está insertada en el lado vertical 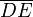$\overline{DE}$ de manera que su movimiento está limitado a desplazamientos sobre dicha varilla. Un segundo resorte de longitud natural nula y constante recuperadora

K 2

conecta la partícula

B

al punto

A

. Los valores de los parámetros del sistema son tales que

K 2 d > m g

.

Considerando que los vínculos son perfectamente lisos, determine las posiciones de las partículas cuando el sistema se halla en equilibrio estático.
Considérese ahora que, mientras que el vínculo en $B$ sigue siendo liso, la partícula sin masa $A$ está sometida a un vínculo rugoso cuya fuerza de rozamiento verifica las leyes del rozamiento seco. ¿Cuáles son las posiciones de equilibrio?

2 Solución

2.1 Equilibrio para vínculos lisos

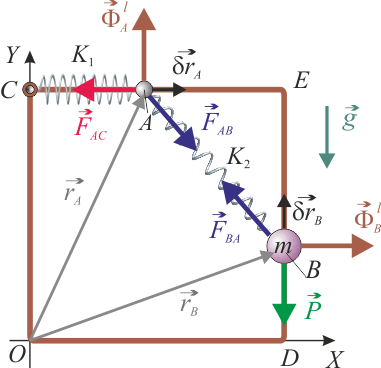
En la figura se muestra el diagrama de fuerzas que actúan sobre cada una de las partículas susceptibles de moverse en el sistema. Como la partícula $A$ no tiene masa, tampoco habrá una fuerza peso actuando sobre ella y sólo estará sometida a la acción del resorte $K 1$ más la acción del vínculo geométrico liso que sólo le permite moverse a lo largo del lado 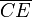$\overline{CE}$ . De esta forma, la descripción analítica de una posición arbitraria del punto $A$ , será:

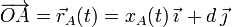
$\overrightarrow{OA}=\vec{r}_A(t)=x_A(t)\!\ \vec{\imath}\!\ + d\!\ \vec{\jmath}$

Comos sabemos, esta acción puede modelarse mediante una fuerza de reacción vincular equivalente, que denominaremos 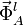$\vec{\Phi}_A^l$ , y que debe ser perpendicular al desplazamiento permitido de la partícula $A$ . Según el sistema de refererencia cartesiano que estamos utilizando, se tendrá:

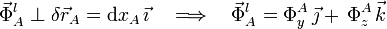
$\vec{\Phi}_A^l\perp\delta\vec{r}_A=\mathrm{d} x_A\!\ \vec{\imath}\quad\Longrightarrow\quad\vec{\Phi}_A^l=\Phi_y^A\!\ \vec{\jmath}+\!\ \Phi_z^A\!\ \vec{k}$

El resorte $K 1$ , de longitud natural nula y con un extremo fijo en $C$ , ejerce sobre $A$ una fuerza con la dirección y el sentido del segmento 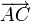$\overrightarrow{AC}$ , y proporcional a su longitud:

$\vec{F}_{AC}=K_1\overrightarrow{AC}=-K_1\!\ x_A(t)\!\ \vec{\imath}=\vec{F}_1$

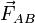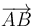Pero también el resorte $K 2$ actúa sobre esta partícula sin masa con una fuerza que denominaremos $\vec{F}_{AB}$ . Como su longitud natural es nula y tine su otro extremo conectado a la partícula $B$ , la correspondiente fuerza será propocional y con igual dirección y sentido que el segmento orientado $\overrightarrow{AB}$ .

$\vec{F}_{AB}=K_2\overrightarrow{AB}=K_2\big[\vec{r}_A(t)-\vec{r}_B(t)\big]$

Es decir, el valor de esta fuerza depende la posición del punto $B$ . Como, por la acción de un vínculo geométrico liso, éste está obligado a desplazarse siempre sobre el lado vertical 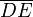$\overline{DE}$ , se tendrá:

$\overrightarrow{OA}=\vec{r}_A(t)=x_A(t)\!\ \vec{\imath}\!\ + d\!\ \vec{k}$

\overrightarrow{OA}=\vec{r}_A(t)=x_A(t)\!\ \vec{\imath}\!\ + d\!\ \vec{\jmath}

Además, por el principio de acción y reacción, se tendrá que sobre la partícula $B$ actuará una fuerza 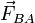$\vec{F}_{BA}$ de igual dirección y módulo que 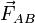$\vec{F}_{AB}$ , pero actuando en sentido contrario:

Cuestión de equilibrio estático, Noviembre 2011

De Laplace

1 Enunciado

2 Solución

2.1 Equilibrio para vínculos lisos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES