Dos masas, un plano y un hilo

De Laplace

Revisión a fecha de 11:42 17 nov 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Diagramas de cuerpo libre
3 Equilibrio sin rozamiento
4 Equilibrio con rozamiento
5 Casos prácticos

1 Enunciado

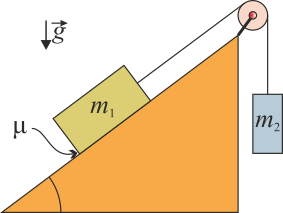
Se tienen dos masas $m 1$ y $m 2$ atadas por un hilo ideal, inextensible y sin masa, que pasa por una polea también ideal (de masa despreciable y sin rozamiento). La masa $m 1$ se encuentra sobre un plano inclinado un ángulo $α$ . La masa $m 2$ cuelga verticalmente.

Suponiendo que no hay rozamiento, determine la aceleración de las masas. ¿Cuál debe ser la relación entre ellas para que el sistema se quede en equilibrio?
Entre la masa $m 1$ y el plano existe un coeficiente de rozamiento (estático y dinámico) $μ$ . ¿Entre qué valores mínimo y máximo debe estar $m 2$ para que las masas queden en equilibrio?
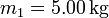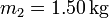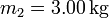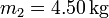Sea $m_1=5.00\,\mathrm{kg}$ , $tg(α) = 0.75$ y $μ = 0.30$ . ¿Cuánto vale la aceleración de las masas si (a) $m_2 = 1.50\,\mathrm{kg}$ , (b) $m_2 =3.00\,\mathrm{kg}$ y (c) $m_2 = 4.50\,\mathrm{kg}$ .

2 Diagramas de cuerpo libre

Analizamos este problema dibujando los diagramas de cuerpo libre de cada una de las masas por separado.

Para la masa 1 (la situada en el plano) actúan las siguientes fuerzas:

Su peso
La reacción normal del plano
La tensión de la cuerda
La fuerza de rozamiento

de forma que su ecuación de movimiento es

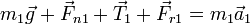
$m_1\vec{g}+\vec{F}_{n1}+\vec{T}_1 + \vec{F}_{r1}=m_1\vec{a}_1$

Sobre la masa 2, la colgante, solo actúan dos fuerzas

Su peso
La tensión de la cuerda

lo que nos da

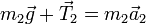
$m_2\vec{g}+\vec{T}_2 = m_2\vec{a}_2$

Por ser la cuerda que una las dos masas inextensible y sin masa, y por ser también ideal la polea (sin masa y sin rozamiento), se cumple en todo instante que

$|\vec{T}_1| = |\vec{T}_2|\qquad\qquad |\vec{a}_1|=|\vec{a}_2|$

La igualdad es entre módulos y no entre vectores, ya que aunque la tensión tenga la misma magnitud, su dirección es diferente para cada masa.

3 Equilibrio sin rozamiento

Consideramos en primer lugar una situación sin rozamiento en la que las masas están perfectamente equilibradas y su aceleración es nula. Esto nos deja con las ecuaciones de equilibrio

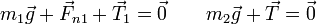
$m_1\vec{g} + \vec{F}_{n1}+\vec{T}_1 = \vec{0}\qquad m_2\vec{g}+\vec{T}=\vec{0}$

Las dos fuerzas que actúan sobre la masa 2 son verticales. Para que se anulen deben ser iguales y opuestas. Esto nos da el valor de la tensión

$-m_2g+T = 0\qquad\Rightarrow\qquad T = m_2g$

Para analizar el estado de la masa 1 consideramos un sistema de ejes en el que el eje X es paralelo al plano hacia arriba, y el eje Z es perpendicular al plano. En este sistema

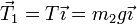
$m_1\vec{g}=-m_1g\,\mathrm{sen}(\alpha)\vec{\imath}-m_1g\cos(\alpha)\vec{k}$ $\vec{F}_{n1}=F_{n}\vec{k}$ $\vec{T}_1=T\vec{\imath}=m_2g\vec{\imath}$

Sustituyendo e igualando a 0 cada componente nos quedan las ecuaciones

$-m_1g\,\mathrm{sen}(\alpha)+m_2g==0\qquad\qquad -m_1g\cos(\alpha)+F_n=0$

lo que nos da la relación buscada

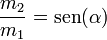
$\frac{m_2}{m_1}= \mathrm{sen}(\alpha)$

También hallamos el valor de la fuerza normal

F n = m 1 g cos(α)

Como caso particular tenemos que si el plano fuera horizontal sería imposible retener las masas. Para que se queden en reposo hace falta rozamiento.

4 Equilibrio con rozamiento

Cuando tenemos en cuenta la fuerza de rozamiento, la ecuación para la masa 1 debe incluir la fuerza correspondiente, que será tangente a la superficie de contacto

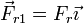
$\vec{F}_{r1}=F_r\vec{\imath}$

En la situación de equilibrio (aceleraciones nulas), quedan las ecuaciones

$-m_1g\,\mathrm{sen}(\alpha)+m_2g+F_r=0\qquad\qquad -m_1g\cos(\alpha)+F_n=0$

El valor de la fuerza de rozamiento no está determinado en principio. Solo sabemos que, en una situación de rozamiento estático

$|F_r|\leq \mu |F_n|= \mu m_1 g\cos(\alpha)\,$

Para hallar las valores máximo y mínimo de la masa 2, debemos considerar las dos posibilidades de deslizamiento inminente:

Que la masa 2 sea tan ligera que no sea capaz de impedir que la masa 1 descienda por el plano.
Que sea tan pesada, que sea capaz de arrastrar a la masa 1 hacia arriba del plano.

En ambos casos las fuerza de rozamiento tiene su valor límite:

$|F_r|= \mu m_1g\cos(\alpha)\,$

pero su sentido puede tener un sentido o el opuesto según el caso. Esto nos lleva a la ecuación de equilibrio

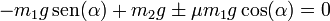
$-m_1g\,\mathrm{sen}(\alpha)+m_2g\pm \mu m_1g\cos(\alpha)=0$

lo que nos da las relaciones

$\frac{m_2}{m_1}= \mathrm{sen}(\alpha)\pm \mu \cos(\alpha)$

siendo los valores máximo y mínimo

$m_{2\mathrm{min}} = m_1(\mathrm{sen}(\alpha)- \mu \cos(\alpha))\qquad\qquad m_{2\mathrm{max}} = m_1(\mathrm{sen}(\alpha)+ \mu \cos(\alpha))$

Al calcular la masa mínima según esta fórmula podría resultar un valor negativo si $μ > tg(α)$ , lo que sería absurdo. Lo que significa esto es que no hace falta masa 2 para que la masa 1 se quede en equilibrio, ya que el rozamiento estático se basta para retener a $m 1$ . Una forma más rigurosa de escribir la masa 2 mínima sería

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): m_{2\mathrm{min}}=\begin{cases} 0 & \mu > \mathrm{tg}(\alpha) \\ m_1(\mathrm{\sen}(\alpha)- \mu \cos(\alpha)) & \mu < \mathrm{tg}(\alpha)\end{cases}

5 Casos prácticos

Dos masas, un plano y un hilo

De Laplace

Contenido

1 Enunciado

2 Diagramas de cuerpo libre

3 Equilibrio sin rozamiento

4 Equilibrio con rozamiento

5 Casos prácticos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES