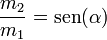Dos masas, un plano y un hilo
De Laplace
Contenido |
1 Enunciado
Se tienen dos masas m1 y m2 atadas por un hilo ideal, inextensible y sin masa, que pasa por una polea también ideal (de masa despreciable y sin rozamiento). La masa m1 se encuentra sobre un plano inclinado un ángulo α. La masa m2 cuelga verticalmente.
- Suponiendo que no hay rozamiento, determine la aceleración de las masas. ¿Cuál debe ser la relación entre ellas para que el sistema se quede en equilibrio?
- Entre la masa m1 y el plano existe un coeficiente de rozamiento (estático y dinámico) μ. ¿Entre qué valores mínimo y máximo debe estar m2 para que las masas queden en equilibrio?
- Sea
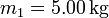 , tg(α) = 0.75 y μ = 0.30. ¿Cuánto vale la aceleración de las masas si (a)
, tg(α) = 0.75 y μ = 0.30. ¿Cuánto vale la aceleración de las masas si (a) 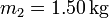 , (b)
, (b) 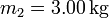 y (c)
y (c) 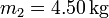 .
.
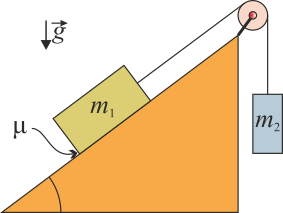
2 Diagramas de cuerpo libre
Analizamos este problema dibujando los diagramas de cuerpo libre de cada una de las masas por separado.
Para la masa 1 (la situada en el plano) actúan las siguientes fuerzas:
- Su peso
- La reacción normal del plano
- La tensión de la cuerda
- La fuerza de rozamiento
de forma que su ecuación de movimiento es
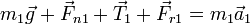
Sobre la masa 2, la colgante, solo actúan dos fuerzas
- Su peso
- La tensión de la cuerda
lo que nos da
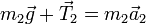
Por ser la cuerda que una las dos masas inextensible y sin masa, y por ser también ideal la polea (sin masa y sin rozamiento), se cumple en todo instante que

La igualdad es entre módulos y no entre vectores, ya que aunque la tensión tenga la misma magnitud, su dirección es diferente para cada masa.
3 Equilibrio sin rozamiento
Consideramos en primer lugar una situación sin rozamiento en la que las masas están perfectamente equilibradas y su aceleración es nula. Esto nos deja con las ecuaciones de equilibrio
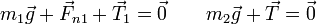
Las dos fuerzas que actúan sobre la masa 2 son verticales. Para que se anulen deben ser iguales y opuestas. Esto nos da el valor de la tensión

Para analizar el estado de la masa 1 consideramos un sistema de ejes en el que el eje X es paralelo al plano hacia arriba, y el eje Z es perpendicular al plano. En este sistema


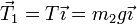
Sustituyendo e igualando a 0 cada componente nos quedan las ecuaciones

lo que nos da la relación buscada