Entrar Página Discusión Historial Go to the site toolbox

Partícula en el interior de un tubo (GIE)

De Laplace

Contenido

1 Enunciado

Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular ω constante alrededor del eje OZ, de forma que la posición de la partícula puede escribirse como

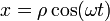
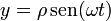
x = \rho\,\mathrm{cos}(\omega t)\,        y= \rho\,\mathrm{sen}(\omega t)

donde 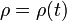\rho = \rho(t)\,, función que hay que determinar, define la posición de la partícula a lo largo del tubo.

  1. Halle la ecuación diferencial que debe satisfacer 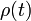\rho(t)\, sabiendo que el tubo no puede ejercer fuerza en la dirección longitudinal (no hay rozamiento).
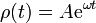
  2. Suponga que \rho(t) =A\mathrm{e}^{\omega t}\,
    1. Compruebe que se trata de una solución de la ecuación diferencial
    2. Calcule la fuerza ejercida por el tubo en cada instante.
    3. Halle las componentes intrínsecas de la aceleración

2 Ecuación para ρ

Si escribimos las ecuaciones de movimiento en polares, separadas en componentes,

\left\{\begin{array}{rcl}m\left(\ddot{\rho}-\rho\dot{\phi}^2\right) & = & F_\rho \\ m\left(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi}\right) & = & F_\varphi\end{array}\right.

tenemos que se simplifican notablemente, teniendo en cuenta los datos del enunciado:

  • El tubo está rotando de forma conocida, es decir, sabemos que el ángulo \varphi varía como
\varphi = \omega t \qquad\Rightarrow\qquad \dot{\varphi}=\omega \qquad\qquad\ddot{\varphi}=0
  • El tubo solo ejerce fuerza mediante el empuje que sus paredes realizan lateralmente sobre la partícula, no a lo largo del propio tubo:
F_\rho = 0\qquad F_\varphi = \Phi

Esto nos deja con

m\left(\ddot{\rho} - \rho\omega^2\right) = 0 \qquad\qquad 2m\omega\dot{\rho}=\Phi

La primera de las dos es la ecuación buscada, ya que nos permite determinar ρ(t)

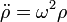
\ddot{\rho}=\omega^2\rho

Una vez que la hemos resuelto, podemos emplear la segunda para calcular la fuerza que ejerce el tubo, que es desconocida apriori

\Phi = 2m\omega\dot{\rho}

3 Análisis de la solución

3.1 Verificación

3.2 Fuerza ejercida por el tubo

3.3 Componentes de la aceleración

Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_en_el_interior_de_un_tubo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace