No Boletín - Adelantamiento entre vehículos (Ex.Nov/11)
De Laplace
1 Enunciado
Dos vehículos (A y B) avanzan por una misma carretera con celeridades variables en el tiempo pero tales que en todo instante se cumple que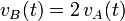 
. El vehículo lento (A) va inicialmente por delante porque partió de un punto más adelantado. En cierto instante, y justo en una curva, el vehículo rápido (B) da alcance al lento (A). ¿Cuáles son las relaciones entre las respectivas aceleraciones tangenciales y entre las respectivas aceleraciones normales de ambos vehículos en el preciso instante del adelantamiento? ¿Son dichas relaciones necesariamente ciertas también para todo instante anterior o posterior al adelantamiento?
2 Solución
Las componentes intrínsecas de la aceleración de una partícula vienen dadas por
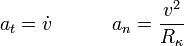
donde 
es la celeridad y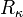 
es el radio de curvatura.
Por tanto, la relación entre las aceleraciones tangenciales de los vehículos A y B se deduce simplemente derivando respecto al tiempo la relación entre sus celeridades:
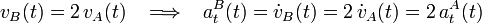
y observamos que esta relación sencilla, por la cual la aceleración tangencial del vehículo rápido es el doble de la aceleración tangencial del vehículo lento, tiene validez para todo instante de tiempo, es decir, en el adelantamiento pero también antes y después del mismo.
En cuanto a las aceleraciones normales de ambos vehículos, podemos escribir:
![v_B(t)=2\,v_A(t)\,\,\,\,\,\Longrightarrow\,\,\,\,\, a_n^B(t)=\frac{[v_B(t)]^2}{R_{\kappa}^B(t)}=\frac{[2\,v_A(t)]^2}{R_{\kappa}^B(t)}=\frac{4\,[v_A(t)]^2}{R_{\kappa}^B(t)}=4\,a_n^A(t)\,\frac{R_{\kappa}^A(t)}{R_{\kappa}^B(t)}](/wiki/images/math/c/c/c/cccdf2eeaf6677343dc90ded3deeb6f1.png)
Ahora bien, en el instante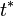 
del adelantamiento ambos vehículos coinciden en un mismo punto de la carretera y por tanto:
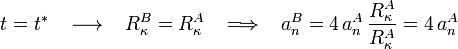
Sin embargo, antes y después del adelantamiento los vehículos A y B se hallarán en puntos distintos de la carretera y, en consecuencia, sus radios de curvatura no coincidirán (salvo casualidades). Por tanto, esa relación sencilla, por la cual la aceleración normal del vehículo rápido es el cuádruple de la aceleración normal del vehículo lento, sólo es necesariamente cierta en el instante del adelantamiento.
