Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del sólido rígido (G.I.T.I.)

De Laplace

Contenido

1 Estudio de la velocidad de tres puntos

En un hipotético sólido rígido, las posiciones y velocidades de tres puntos son respectivamente:

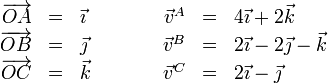
\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}&\qquad & \vec{v}^A & = & 4\vec{\imath}+2\vec{k}\\ \overrightarrow{OB}&=&\vec{\jmath}&\qquad & \vec{v}^B& = &2\vec{\imath}-2\vec{\jmath}-\vec{k}\\ \overrightarrow{OC}&=&\vec{k}&\qquad & \vec{v}^C&=&2\vec{\imath}-\vec{\jmath} \end{array}
  1. Demuestre que estas velocidades son compatibles con la condición de rigidez.
  2. Halle la velocidad del punto O(0,0,0).
  3. Calcule la velocidad del punto \overrightarrow{OP}=2\vec{\imath}-2\vec{\jmath}-\vec{k}.
  4. ¿Existe algún punto que tenga velocidad nula? ¿Dónde estaría situado?

Todas las cantidades están expresadas en las unidades del SI.

2 Ejemplo de campo de velocidades de un sólido

Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,

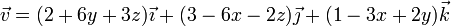
\vec{v}=(2 + 6 y + 3 z)\vec{\imath}+(3 - 6 x - 2 z)\vec{\jmath}+(1 - 3 x + 2 y)\vec{k}
  1. Pruebe que corresponde al movimiento de un sólido rígido.
  2. Determine la velocidad angular y la velocidad de deslizamiento.
  3. Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.

Todas las cantidades están expresadas en las unidades del SI.

3 Velocidad de tres puntos de un sólido

Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,

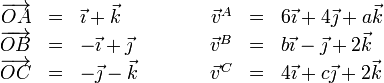
\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & \vec{v}^A & = & 6\vec{\imath}+4\vec{\jmath}+a\vec{k}\\ \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & \vec{v}^B& = & b\vec{\imath}-\vec{\jmath}+2\vec{k}\\ \overrightarrow{OC}&=&-\vec{\jmath}-\vec{k}&\qquad & \vec{v}^C&=&4\vec{\imath}+c\vec{\jmath}+2\vec{k} \end{array}
  1. Halle los valores de a, b, c.
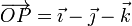  2. Halle la velocidad del punto \overrightarrow{OP}=\vec{\imath}-\vec{\jmath}-\vec{k}.
  3. Calcule la velocidad angular y la de deslizamiento
  4. Determine la posición del eje instantáneo de rotación.

Todas las cantidades están expresadas en las unidades del SI.

4 Análisis de la velocidad de dos puntos de un sólido

Las velocidades, 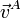\vec{v}^{A} y \vec{v}^{B}, de sendos puntos, A y B, de un sólido rígido respecto a un sistema de referencia fijo OXYZ han sido medidas en tres experimentos distintos. En todos ellos, los puntos A y B ocupaban idénticas posiciones respecto al triedro OXYZ, definidas por las coordenadas A(1,0,0) y B(0,1,0), respectivamente. Las velocidades medidas en los tres experimentos vienen dadas (en la base de OXYZ) por los siguientes pares de vectores:

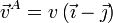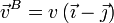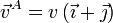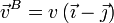  • a: \vec{v}^{A}= v \,(\vec{\imath} - \vec{\jmath}); \vec{v}^{B}= v \,(\vec{\imath} - \vec{\jmath}).
  • b: \vec{v}^{A}= v \,(\vec{\imath} + \vec{\jmath}); \vec{v}^{B}= v \,(\vec{\imath} - \vec{\jmath}).
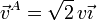  • c: \vec{v}^{A}= \sqrt{2}\,v \vec{\imath}; \vec{v}^{B}= \sqrt{2}\,v \vec{\imath}.

Si se sabe que cada una de las situaciones medidas corresponde a uno de los casos siguientes:

  1. Se ha producido un error en las medidas.
  2. La velocidad de deslizamiento es v\,.
  3. El eje instantáneo de rotación y mínimo deslizamiento pasa por A y B.

establezca razonadamente la relación de correspondencia entre los experimentos y los diferentes casos posibles.

5 Sólido en rotación instantánea

Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 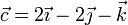\vec{c}=2\vec{\imath}-2\vec{\jmath}-\vec{k}, de tal forma que la velocidad del punto B(0,2,1) es

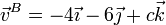
\vec{v}^B=-4\vec{\imath}-6\vec{\jmath}+c\vec{k}
  1. Halle el valor de la constante c.
  2. Calcule la velocidad angular instantánea.
  3. Calcule la velocidad del punto C(1,1,0).

Todas las cantidades están expresadas en las unidades del SI.

6 Identificación de posibles movimientos rígidos

En un hipotético sólido rígido, consideramos los puntos

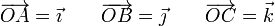
\overrightarrow{OA}=\vec{\imath}\qquad\overrightarrow{OB}=\vec{\jmath}\qquad\overrightarrow{OC}=\vec{k}

y analizamos los casos correspondientes a las siguientes velocidades para los tres puntos:

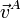
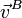
Caso \vec{v}^A \vec{v}^B \vec{v}^C
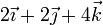
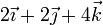
I 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{k}
II 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath} 2\vec{\imath}+4\vec{\jmath} + 2\vec{k}
III 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k}
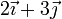
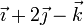
IV 2\vec{\imath}+3\vec{\jmath} \vec{\imath}+2\vec{\jmath}-\vec{k} 4\vec{\imath}+4\vec{\jmath}+2\vec{k}
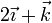
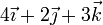
V 2\vec{\imath}+\vec{k} 4\vec{\imath}+2\vec{\jmath}+3\vec{k} 3\vec{\imath}+\vec{\jmath}+2\vec{k}
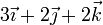
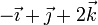
VI 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath}+2\vec{k} -\vec{\imath}+\vec{\jmath}+2\vec{k}

Todas las cantidades están expresadas en las unidades del SI.

Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.

7 Triángulo en movimiento helicoidal

El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos:

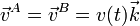  • Los vértices A y B permanecen en todo instante sobre el eje OZ, desplazándose ambos con igual velocidad instantánea: \vec{v}^A = \vec{v}^B = v(t) \vec{k}.
  • El vértice C se mueve describiendo la hélice Γ, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde A y b son constantes conocidas):
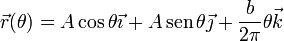
\vec{r}(\theta)= A\cos\theta\vec{\imath}+A\,\mathrm{sen}\,\theta\vec{\jmath}+ \frac{b}{2\pi}\theta\vec{k}
  1. Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado.
  2. Exprese, en función de los datos del enunciado, la componente normal de la aceleración del vértice C en un instante cualquiera.
  3. Para el caso en que v(t) = v0 (cte), y 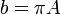\, b = \pi A, calcule la aceleración del vértice C. Determine la ley horaria s = s(t) con que el punto C describe su trayectoria.

8 Rodadura permanente de un disco

La rodadura permanente de un disco de radio R sobre una superficie horizontal puede describirse mediante el campo de velocidades

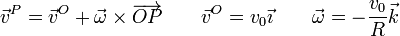
\vec{v}^P = \vec{v}^O +\vec{\omega}\times\overrightarrow{OP}\qquad\vec{v}^O = v_0\vec{\imath}\qquad\vec{\omega}=-\frac{v_0}{R}\vec{k}

donde la superficie horizontal se encuentra en y = − R.

  1. Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco.
  2. Suponiendo 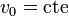v_0=\mathrm{cte}\,, calcule la aceleración de dichos puntos para el mismo instante.

9 Ejemplo de movimiento de precesión

El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular

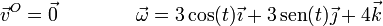
\vec{v}^O =\vec{0}\qquad\qquad\vec{\omega}=3\cos(t)\vec{\imath}+3\,\mathrm{sen}(t)\vec{\jmath}+4\vec{k}

Consideremos el punto 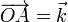\overrightarrow{OA}=\vec{k}

  1. Determine la velocidad de este punto en cada instante.
  2. Determine la aceleración de A en todo instante.
  3. Halle, para cada instante, las componentes intrínsecas de la aceleración y el radio de curvatura en el mismo punto.

Todas las cantidades están expresadas en las unidades del SI.

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_s%C3%B3lido_r%C3%ADgido_(G.I.T.I.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace