Entrar Página Discusión Historial Go to the site toolbox

3.12. Equilibrio de partícula en hélice

De Laplace

Contenido

1 Enunciado

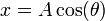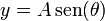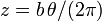Una partícula de masa m se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante k y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada en la hélice de ecuaciones x = A\,\mathrm{cos}(\theta), y = A\,\mathrm{sen}(\theta), z = b\,\theta/(2\pi).

  1. Determine la posición de equilibrio de la partícula sobre la hélice.
  2. Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio.
  3. Determine la energía potencial como función del parámetro \theta\, y discuta la estabilidad de la posición de equilibrio.

2 Equilibrio

La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle y la fuerza de reacción vincular. En el equilibrio, la resultante debe ser nula

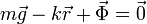
m\vec{g}-k\vec{r}+\vec{\Phi}=\vec{0}

Expresando las tres fuerzas en la base cartesiana ortonormal, se tiene

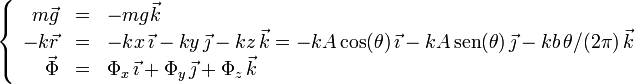
\left\{\begin{array}{rcl} m\vec{g} & = & -mg\vec{k} \\ -k\vec{r} & = & -kx\,\vec{\imath}-ky\,\vec{\jmath}-kz\,\vec{k} = -kA\,\mathrm{cos}(\theta)\,\vec{\imath}-kA\,\mathrm{sen}(\theta)\,\vec{\jmath}-kb\,\theta/(2\pi)\,\vec{k} \\ \vec{\Phi} & = & \Phi_x\,\vec{\imath}+\Phi_y\,\vec{\jmath}+\Phi_z\,\vec{k} \end{array}\right.

Junto a esta ecuación tenemos la del vínculo

\vec{r} = A\,\mathrm{cos}(\theta)\,\vec{\imath}+A\,\mathrm{sen}(\theta)\,\vec{\jmath}+b\,\theta/(2\pi)\,\vec{k}

Separando en las componentes cartesianas tenemos, para el peso

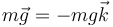
m\vec{g}=-mg\vec{k}

para la fuerza elástica

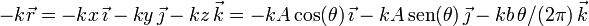
-k\vec{r} = -kx\,\vec{\imath}-ky\,\vec{\jmath}-kz\,\vec{k} = -kA\,\mathrm{cos}(\theta)\,\vec{\imath}-kA\,\mathrm{sen}(\theta)\,\vec{\jmath}-kb\,\theta/(2\pi)\,\vec{k}

y para la fuerza de reacción vincular

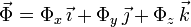
\vec{\Phi} = \Phi_x\,\vec{\imath}+\Phi_y\,\vec{\jmath}+\Phi_z\,\vec{k}

La fuerza de reacción vincular va en la dirección normal a la hélice (pues no se menciona que exista rozamiento, es decir, se sobreentiende que la hélice es un vínculo liso). Un vector tangente a la hélice es

\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta} = -A\,\mathrm{sen}(\theta)\,\vec{\imath}+A\,\mathrm{cos}(\theta)\,\vec{\jmath}+b/(2\pi)\,\vec{k}

3 Fuerza de reacción vincular

4 Energía potencial y estabilidad del equilibrio

Obtenido de "http://tesla.us.es/wiki/index.php/3.12._Equilibrio_de_part%C3%ADcula_en_h%C3%A9lice"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace