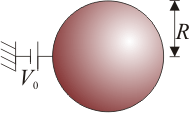
Capacidad de una esfera

De Laplace

1 Enunciado

Una esfera metálica de radio a se encuentra a potencial V₀ respecto al infinito. No hay más conductores en el sistema. Determine el potencial y el campo eléctrico en todos los puntos del espacio, así como la carga almacenada en la esfera conductora.

2 Solución

Este es el problema más sencillo que se puede plantear en problemas de campo eléctrico en presencia de conductores, ya que, como veremos, depende de una sola variable y no requiere hacer aproximación alguna.

La esfera se encuentra conectada a un generador que la sitúa a un cierto potencial eléctrico. Para conseguir esto, el generador coloca cargas en la esfera, las cuales se dispondrán en la superficie de ésta. Estas cargas provocan un campo eléctrico en el exterior. En el interior, en cambio, el potencial será constante y el campo eléctrico nulo.

        

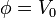
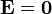
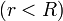
Para hallar el campo eléctrico exterior, debemos resolver la ecuación de Poisson, pero, dado que no hay más carga en el exterior, ésta se reduce a la ecuación de Laplace

    

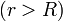
con las condiciones de contorno de que en la superficie de la esfera el potencial está fijado

    

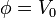
y de que en el infinito, que tomamos como origen de potencial, el potencial se anula

    

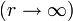
La geometría del sistema sugiere el uso de coordenadas esféricas, en las cuales la ecuación de Laplace se escribe

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{1}{r^2}\,\frac{\partial\ }{\partial r}\left(r^2\frac{\partial\phi}{\partial r}\right) + \frac{1}{r^2\operatorname{sen}\theta}}\,\frac{\partial\ }{\partial \theta}\left(\operatorname{sen}\theta\frac{\partial\phi}{\partial \theta}\right) =0