Caso de movimiento circular

De Laplace

1 Enunciado

Una partícula describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple

con k una constante y el ángulo que el vector de posición instantánea forma con el eje OX.

1. Determine la aceleración angular de la partícula como función del ángulo .
2. Halle las componentes intrínsecas de la aceleración lineal en 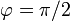y .
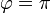3. Determine la ley horaria .

2 Aceleración angular

3 Componentes intrínsecas

4 Ley horaria
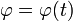