Entrar Página Discusión Historial Go to the site toolbox

Ejemplo de movimiento expresado en polares

De Laplace

Contenido

1 Enunciado

Una partícula describe una curva cuya ecuación en coordenadas polares es

\rho = A\cos(\omega t)\qquad\qquad \varphi = \omega t
  1. Calcule la velocidad y la aceleración en cada instante.
  2. Halle las componentes intrínsecas de la aceleración para todo t.
  3. Calcule el radio y el centro de curvatura en todo momento.
  4. ¿De qué tipo de movimiento se trata?

2 Velocidad y aceleración

2.1 Velocidad

La expresión de la velocidad empleando coordenadas polares es

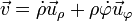
\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\varphi}\vec{u}_\varphi

donde, en este caso

\rho = A\cos(\omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\omega A\,\mathrm{sen}(\omega t)\qquad\qquad\varphi = \omega t\qquad \dot{\varphi}\equiv\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega

que, sustituyendo nos da

\vec{v}=\omega A\left(-\mathrm{sen}(\omega t)\vec{u}_\rho+\cos(\omega t)\vec{u}_\varphi\right)

2.2 Aceleración

3 Componentes intrínsecas

3.1 Tangencial

3.2 Normal

4 Radio y centro de curvatura

4.1 Radio de curvatura

4.2 Centro de curvatura

5 Identificación del movimiento

Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplo_de_movimiento_expresado_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace