Fusible de plomo

De Laplace

Revisión a fecha de 16:12 10 jul 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Corriente máxima
- 2.2 Resistencia del plomo

1 Enunciado

Para construir un fusible se intercala un hilo de plomo (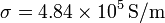 $\sigma = 4.84\times 10^5\,\mathrm{S}/\mathrm{m}$ ) en el camino de un hilo de cobre de 0.5mm de radio. La pieza de plomo está formado por un hilo de 0.1mm de radio y 1cm de longitud, unido al cobre por dos troncos de cono, también de plomo, de 0.5cm de longitud.

La condición de fusión la da el que en un intervalo de tiempo de 1s, en la pieza de plomo se disipe una energía de 700mJ/mm³. Calcule la intensidad máxima que puede circular por el hilo de cobre para que no se alcance este límite.
Calcule la resistencia de la pieza de plomo, admitiendo que el sistema se comporta como un conductor filiforme de sección variable.

2 Solución

2.1 Corriente máxima

Para calcular la corriente máxima admisible no necesitamos considerar el efecto de los dos troncos de cono, ya que la densidad de corriente máxima se dará en la parte más estrecha del circuito, y ésta es el hilo central.

El hilo central es un conductor filiforme, y por tanto podemos suponer que la densidad de corriente es uniforme en todo su volumen.

El dato que se nos da como condición de fusión es la energía disipada por unidad de volumen (se mide en J/m³) durante un intervalo de tiempo de 1s. De aquí que la potencia máxima que se puede disipar por unidad de volumen es

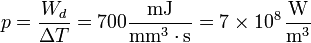
$p = \frac{W_d}{\Delta T} = 700\frac{\mathrm{mJ}}{\mathrm{mm}^3\cdot \mathrm{s}} = 7\times 10^8\,\frac{\mathrm{W}}{\mathrm{m}^3}$

Para hallar la densidad de corriente máxima igualamos esta potencia disipada por unidad de volumen a la expresión de la ley de Joule

$p = \sigma E^2 =\mathbf{E}\cdot\mathbf{J} = \frac{J^2}{\sigma}$

Igualando y despejando

$J = \sqrt{\sigma p} = 1.84\times 10^7\,\frac{\mathrm{A}}{\mathrm{m}^2}$

De esta densidad de corriente obtenemos la intensaidad máxima que puede circular por el hilo de plomo, que es la misma que la que pasa por el hilo de cobre, pues están en serie:

$I_\mathrm{max}=\int \mathbf{J}\cdot\mathrm{d}\mathbf{S} = J\pi a^2 = 0.58\,\mathrm{A}$

2.2 Resistencia del plomo

Para hallar la resistencia de la pieza de plomo, la descomponemos en tres elementos en serie: los dos troncos de cono y el hilo central. La resistencia de los dos troncos de cono es la misma, por lo que la resistencia total será

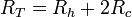
$R_T = R_h + 2R_c\,$

La resistencia del hilo es inmediata, por ser su sección constante

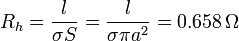
$R_h = \frac{l}{\sigma S} = \frac{l}{\sigma \pi a^2} = 0.658\,\Omega$

Para los troncos de cono, teniendo en cuenta que su longitud (0.5cm) es mucho mayor que su anchura (0.5mm) también podemos aproximar su valor por el de un conductor, pero ahora de sección variable

$R_c = \int \frac{\mathrm{d}l}{\sigma S}$

En este caso $d l = d x$ siendo $x$ la coordenada a lo largo del hilo por su centro. La sección es

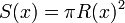
$S(x) = \pi R(x)^2\,$

donde el radio varía linealmente desde $b$ , en $x = 0$ , a $a$ , en $x = l$ , esto es

$R(x) = a + \frac{x}{l}(b-a)$

resultando una resistencia

$R_c = \int_0^l \frac{\mathrm{d}x}{\sigma \pi (a+(x/l)(b-a))^2} = -\left.\frac{l}{\sigma\pi (b-a)(a+(x/l)(b-a))}\right|_0^l = \frac{l}{\sigma \pi a b} = 0.066\,\Omega$

Sumando queda la resistencia total

$R_T = R_h + 2R_c = 0.789\,\Omega$

Fusible de plomo

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Corriente máxima

2.2 Resistencia del plomo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES