Aproximación numérica de la velocidad y la aceleración
De Laplace
Revisión a fecha de 19:02 8 oct 2011; Antonio (Discusión | contribuciones)
1 Enunciado
La posición de una partícula en distintos instantes de tiempo es, aproximadamente
| t (s) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x (m) | 0.00 | -0.04 | -0.06 | -0.06 | -0.04 | 0.00 | 0.06 | 0.14 | 0.24 | 0.36 | 0.50 |
- ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre
 y
y  .
.
- Calcule aproximadamente la aceleración en el mismo intervalo.
2 Velocidad
La velocidad instantánea es la derivada de la posición respecto al tiempo. Si no conocemos la posición como una función, sino solo como una lista de datos (lo que se llama un muestreo) podemos aproximar la derivada por el cociente entre incrementos.
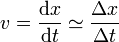
Podemos construir entonces una tabla de valores aproximados de la velocidad hallando las diferencias de posiciones y tiempos entre instantes sucesivos de la lista y calculando su cociente. Nos quedaría entonces la tabla siguiente
| t (s) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x (m) | 0.00 | -0.04 | -0.06 | -0.06 | -0.04 | 0.00 | 0.06 | 0.14 | 0.24 | 0.36 | 0.50 |
| Δx (m) | -0.04 | -0.02 | -0.00 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | |
| v (m/s) | -0.4 | -0.2 | -0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
Una mejor aproximación sería asignar estas velocidades no al instante inicial de cada intervalo, sino al punto medio de cada uno, esto es, quedaría como
| t (s) | 0.05 | 0.15 | 0.25 | 0.35 | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 | 0.95 |
|---|---|---|---|---|---|---|---|---|---|---|
| v (m/s) | -0.4 | -0.2 | -0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |





