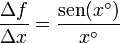Entrar Página Discusión Historial Go to the site toolbox

Cálculo numérico de la derivada del seno

De Laplace

1 Enunciado

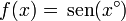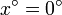Se trata de calcular la derivada de f(x)=\,\mathrm{sen}(x^\circ) para x^\circ=0^\circ.

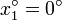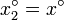  1. Exprese el cociente Δf / Δx, cuando x_1^\circ=0^\circ y x_2^\circ=x^\circ.
  2. Calcule numéricamente el cociente anterior para 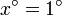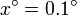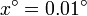x^\circ=1^\circ, x^\circ=0.1^\circ, x^\circ=0.01^\circ,… hasta 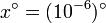x^\circ=(10^{-6})^\circ. ¿A cuanto tiende el límite?
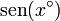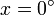  3. Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de \mathrm{sen}(x^\circ) en x=0^\circ?

2 Cociente incremental

La derivada de una función equivale al límite del cociente entre incrementos cuando estos tienden a cero

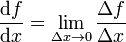
\frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x}

En nuestro caso, consideramos un incremento entre 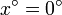x^\circ = 0^\circ y un cierto valor del ángulo

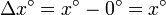
\Delta x^\circ = x^\circ - 0^\circ = x^\circ

mientras que el incremento en la función es

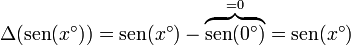
\Delta(\mathrm{sen}(x^\circ))=\mathrm{sen}(x^\circ)-\overbrace{\mathrm{sen}(0^\circ)}^{=0}= \mathrm{sen}(x^\circ)

Por tanto, el cociente entre incrementos se reduce a

\frac{\Delta f}{\Delta x}=\frac{\mathrm{sen}(x^\circ)}{x^\circ}
Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_num%C3%A9rico_de_la_derivada_del_seno"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace