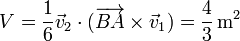Volumen de un tetraedro (G.I.A.)
De Laplace
1 Enunciado
Halla el volumen de un tetraedro del cuál se sabe que las coordenadas
cartesianas de dos de sus vértices se corresponden con las ternas
A(0,1,1) y B(2, − 1,2), y que dos de las aristas que concurren en B
están definidas por los vectores libres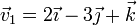 
y
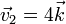(las coordenadas están en metros).
2 Solución
El vector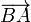 
es
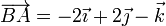
Podemos verificar que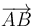 
, 
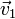y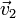 
no son
colineales calculando su producto mixto
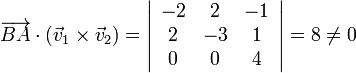
En cada vértice de un tetraedro concurren tres aristas, luego estos tres vectores son las aristas que concurren en B. Esto nos define el tetraedro completo, como se muestra en la figura
El volumen de un tetraedro
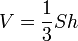
donde S es el área de una de las caras y h es la altura, es decir, la distancia entre esa cara y el vértice opuesto.
Si consideramos como base la cara formada por los vectores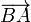
y 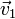, su área es
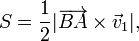
mientras que la altura h es precisamente la proyección de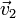
sobre la dirección del vector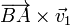 
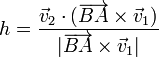
Sustituyendo queda
