Producto mixto nulo (G.I.A.)
De Laplace
Revisión a fecha de 16:06 4 oct 2011; Pedro (Discusión | contribuciones)
Contenido |
1 Enunciado
Dados los vectores 
, 
y 
,
demuestra que la relación
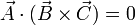se cumple en cualquiera de los siguientes supuestos:
- Los tres vectores son colineales.
- Dos de los vectores son colineales.
- , y no son colineales pero sí coplanarios.
2 Solución
Veamos cada uno de los casos
2.1 Los tres vectores colineales
En este caso y son paralelos, por lo que su
producto vectorial es nulo,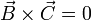 
, con lo
cual se cumple la igualdad.
2.2 Dos vectores colineales
Si y son colineales recuperamos el caso anterior.
Supongamos que y son colineales. Como
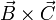es perpendicular a y
, el producto escalar
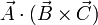es nulo, pues
también es perpendicular al producto vectorial. Lo mismo
ocurre si y son paralelos.
2.3 Coplanarios
El producto vectorial 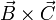es perpendicular al
plano definido por y . Por tanto es
perpendicular a , por lo que la igualdad se cumple.
