Ejemplos de estimaciones numéricas
De Laplace
Contenido |
1 Enunciado
Estime las siguientes cantidades:
- El número de latidos del corazón de una persona a lo largo de su vida.
- Las bolas que hay en la máquina de la figura.
- La velocidad de reproducción en bits/s de un CD de música.

2 Latidos del corazón
La estimación es sencilla: multiplicamos lo que dura una vida en minutos por el número de latidos por minuto.
La esperanza de vida en España ronda los 80 años (un poco más para mujeres y un poco menos para hombres), así que podemos aproximar el número de minutos en una vida por
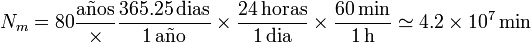
esto es, 42 millones de minutos.
Multiplicando por un ritmo cardíaco de unos 70 latidos por minuto nos queda
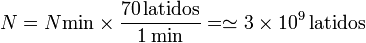
Tres mil millones de latidos como promedio para una vida de 80 años.
Evidentemente hay variaciones debido a las diferencias en longevidad, en las variaciones del ritmo cardiaco a lo largo de la vida, etc. pero una estimación de entre dos y tres mil millones de latidos es bastante razonable.
3 Bolas en la máquina
Veamos primero la imagen en grande:

Vemos que el recipiente es un prisma más o menos cúbico, cuya arista horizontal mide aproximadamente 6 diámetros de las bolas y su altura unos 7 por lo que su volumen será

El volumen ocupado por cada bola, si no contamos los intersticios sería
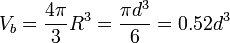
Si contamos los intersticios, el volumen correspondiente a cada bola es algo mayor. Podemos estimar este volumen como una cantidad intermedia entre lo que tendría la bola sola y el que tendría un cubo de lado d (es claro que las bolas se empaquetan más que si fueran cubitos). Así que un valor razonable para el volumen efectivo sería la media entre 0.5d3 y d3
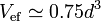
y el número de bolas sería
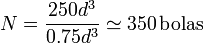
Observemos que no necesitamos saber el diámetro de cada bola, ya que los factores correspondientes se cancelan.
La división daría realmente 333 pero eso es un exceso de cifras significativas, pues ni el tamaño de la caja ni el volumen de cada bola son cantidades que conozcamos más allá de la primera cifra, con una amplia incertidumbre en la segunda. Lo más que podemos decir es que el número de bolas estaría entre 300 y 400 bolas.
4 Velocidad de reproducción
La velocidad de reproducción es sencilla: simplemente dividimos el número de bits de un CD por el tiempo que se emplea en reproducirlo.
La capacidad de un CD es conocida, ya que viene en todas las cajas, o lo sabe cualquiera que haya manejado un fichero “ripeado” de una serie o película: 700MB. Pasando esto a bits queda
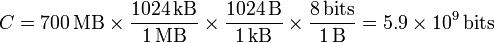
¿Cuánto dura un CD de música? Suele venir también en las etiquetas. Si no, puede ser interesante saber que se dice que su tamaño fue fijado de forma que cupiera la novena sinfonía de Beethoven, que dura 74 minutos. En cualquier la duración de un CD es de unos 80 minutos, o 4800 segundos. Por tanto
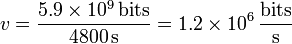
Vemos que es algo superior a un megabit por segundo. Un valor exacto obtenido a partir de la frecuencia de muestreo es de 1411.2 kbit/s.





