Fuerzas de rozamiento (GIE)
De Laplace
Contenido |
1 Introducción
Una categoría de fuerzas que aparecen en casi todos los problemas de dinámica, tanto de la partícula como del sólido, es la de las fuerzas de rozamiento. La presencia de estas fuerzas es inevitable, como garantiza el segundo principio de la termodinámica, si bien en ocasiones pueden considerarse como despreciables o ausentes.
Estas fuerzas son difíciles de modelar ya que sus causas son variadas y no obedecen a una teoría física sencilla. Por ello, aquí nos limitaremos a describir cualitativamente los casos más frecuentes.
2 Rozamiento seco
El rozamiento seco es el producido entre dos superficies, no lubricadas, en contacto. El típico ejemplo es un bloque apoyado sobre un plano horizontal o inclinado.
Este rozamiento se produce debido a que los átomos de uno y otro sólido forman pequeños enlaces temporales, que es necesario romper para conseguir el desplazamiento relativo. Estos enlaces se forman debido a las irregularidades del material, a la presión con la que se forma el contacto y al área de la superficie de contacto.
La fuerza de rozamiento seco tiende dos modalidades:
- Rozamiento estático: se produce cuando las dos superficies están en reposo relativo
- Rozamiento dinámico: se da cuando una de las superficies desliza sobre la otra.
2.1 Rozamiento estático
El rozamiento estático posee las siguientes propiedades:
- Es tangente a la superficie de contacto.
- Posee un valor máximo, proporcional a la componente normal de la fuerza aplicada entre los dos cuerpos

- siendo μ una magnitud adimensional conocida como coeficiente de rozamiento estático. Su valor depende de los dos materiales que estén en contacto:
| Material 1 | Material 2 | μ |
|---|---|---|
| Madera | Cemento | 0.6 |
| Madera | Madera | 0.25−0.5 |
| Goma | Cemento | 1.0 |
| Teflón | Teflón | 0.04 |
| Acero | Acero | 0.80 |
Es un error común el pensar que el coeficiente de rozamiento no puede superar a la unidad. Sí, puede hacerlo (el de goma sobre materiales muy abrasivos puede llegar a 4). No hay ningún impedimento físico para que la fuerza de rozamiento supere en módulo a la fuerza normal.
La ley de rozamiento estático nos da un valor máximo para la fuerza de rozamiento, no nos dice cuánto vale ésta.
Supongamos que tenemos un bloque de madera de 5 kg en reposo sobre el suelo de cemento y aplicamos lateralmente una fuerza de 10 N. ¿Se moverá el bloque? El valor máximo de la fuerza de rozamiento es
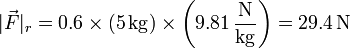
Pero naturalmente eso no es lo que vale la fuerza de rozamiento en este caso concreto, ya que si tuviera dicho valor, superaría a la fuerza aplicada y el bloque se movería en la dirección opuesta a la que se le empuja, lo que es absurdo. Lo que nos dice este resultado es que, puesto que el valor máximo supera a la fuerza aplicada, el bloque no se mueve. La fuerza de rozamiento vale, en este caso, 10 N (igual a la fuerza aplicada).
Si la fuerza aplicada hubiera sido de 40 N, este resultado nos diría que el rozamiento no es capaz de oponerse a la fuerza aplicada y el bloque empieza a moverse, momento a partir del cual se aplica la ley del rozamiento dinámico.
La situación en la que la fuerza de rozamiento alcanza su valor máximo se denomina de deslizamiento inminente, ya que una fuerza aplicada ligeramente superior a las de esta configuración es capaz de conseguir el deslizamiento de las superficies.
Asociado a la fuerza de rozamiento se encuentra el ángulo de fricción β definido por la relación

Este ángulo equivale a la mayor inclinación que puede tener un plano inclinado antes de que un bloque situado sobre él comience a deslizar, esto es, se encuentre en posición de deslizamiento inminente. Esta relacion permite medir experimentalmente el coeficiente de rozamiento empleando un plano de inclinación variable, que se va elevando lentamente hasta que se produzca deslizamiento.
Gráficamente, el que la fuerza de rozamiento tenga un valor máximo quiere decir que para que la fricción consiga oponerse al resto de fuerzas aplicadas, la resultante de todas ellas (sin contar a la propia fuerza de rozamiento), debe hallarse dentro de un cono con vértice el punto de contacto y de ángulo de apertura β. Si la resultante queda fuera, se produce deslizamiento.
2.2 Rozamiento dinámico
El rozamiento dinámico o por deslizamiento se produce cuando una superficie desliza sobra sobre otra.
Este rozamiento se debe también a los enlaces que se forman entre átomos de ambos materiales. Sin embargo, al ser estos enlaces de menor duración, por el movimiento relativo, la fuerza de rozamiento estático es inferior que la máxima posible en el caso estático.
La fuerza de rozamiento dinámico verifica aproximadamente las siguientes propiedades:
- El proporcional a la fuerza aplicada
- Es independiente de la velocidad relativa
- Va en sentido opuesto a la velocidad relativa
La proporcionalidad puede expresarse por la relación
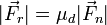
siendo μd el coeficiente de rozamiento dinámico, que será inferior al estático para los mismos materiales. De nuevo, no hay ninguna condición de que sea inferior a la unidad (aunque suele serlo).
| Material 1 | Material | μ |
|---|---|---|
| Madera | Madera | 0.4−0.5 |
| Goma | Cemento | 0.6−0.8 |
| Teflón | Teflón | 0.04 |
| Acero | Acero | 0.16 |
Asociado al coeficiente de rozamiento dinámico se encuentra otro ángulo de rozamiento

que sería el ángulo que debe tener un plano inclinado para que un bloque descienda por él a velocidad constante.
Si representamos conjuntamente la fuerza de rozamiento estático y de rozamiento dinámico, para un bloque, como función de la fuerza tangencial aplicada, obtenemos una gráfica como la de la figura






