Sistema de dos bloques conductores
De Laplace
Contenido |
1 Enunciado
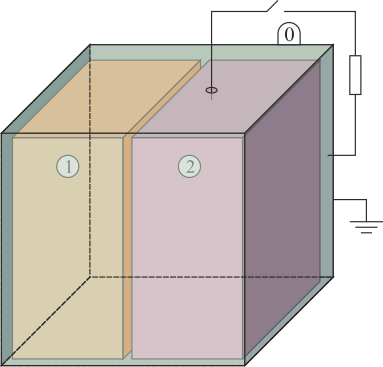
Se tiene un sistema de conductores formado por dos prismas (“1” y “2”), de dimensiones 50 mm×50 mm×25 mm, separados una distancia de 1 mm. Envolviendo a estos dos volúmenes se encuentra una caja cúbica, separada de los bloques por un espacio de 1 mm. Esta caja se encuentra permanentemente a tierra y sirve de eferencia de potencial. Entre los bloques y la caja exterior hay un dieléctrico ideal de permitividad 30 pF/m.
- Determine los coeficientes de capacidad e inducción, Cik, del sistema de dos bloques. Desprecie los efectos de borde.
- Suponga que en un momento dado los dos conductores están aislados. El “1” almacena una carga 18 nC, mientras que el otro está descargado. Halle el potencial de cada bloque en esta situación, así como la carga en la caja exterior. Calcule la energía almacenada en el sistema.
- Suponga que, en la situación anterior, se conecta el bloque descargado a la caja exterior mediante un cable de resistencia 10 Ω. Halle las cargas y potenciales de los bloques y la caja exterior una vez alcanzado de nuevo el equilibrio electrostático. Calcule la energía final del sistema.
- Halle la corriente que circula por el cable de conexión como función del tiempo, así como la energía disipada por efecto Joule. ¿Cuánto tiempo tarda aproximadamente en alcanzarse el nuevo equilibrio electrostático?
2 Coeficientes de capacidad
La forma más sencilla de calcular los coeficientes de capacidad e inducción es mediante el circuito equivalente.
El circuito equivalente está formado por dos nodos y tres condensadores. Los nodos representan a los dos bloques. Los condensadores son uno de capacidad 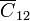 entre ambos nodos y que representa las líneas de campo que van de un bloque a otro, y dos condensadores
entre ambos nodos y que representa las líneas de campo que van de un bloque a otro, y dos condensadores 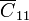 y
y 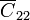 , que representan las líneas de campo que conectan cada bloque con la caja exterior.
, que representan las líneas de campo que conectan cada bloque con la caja exterior.
Para hallar los valores de las capacidades, despreciamos los efectos de borde, por lo que se pueden tratar como una asociación de condensadores planos. Si tomamos como unidad un condensador cuya superficie sea un rectángulo de 25 mm×50 mm y distancia entre placas 1 mm, con capacidad
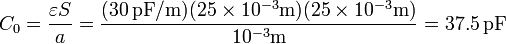
Entonces, el condensador que forman los dos bloques tiene el doble de esta área y por tanto el doble de capacidad
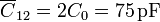
Los que forma cada bloque con la caja exterior equivale a 6 veces el condensador unidad (2 veces en la cara cuadrada y las 4 caras laterales)
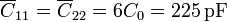
Una vez que tenemos las capacidades es inmediato hallar los coeficientes de capacidad
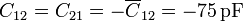
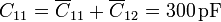
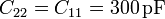
o, en forma matricial
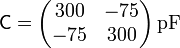
3 Estado de equilibrio inicial
En el estado inicial conocemos la carga de los dos conductores

y se trata de hallar las respectivas tensiones. Si expresamos la carga en picoculombios, el voltaje en voltios y la capacidad en picofaradios, nos queda el sistema
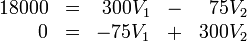
Despejando en la segunda y sustituyendo en la primera
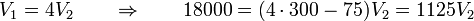
y de aquí

La energía almacenada en el sistema es igual a
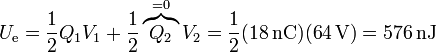
La carga almacenada en las paredes de la caja exterior, por el teorema de Faraday, es igual a la carga contenida en su interior, cambiada de signo
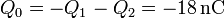
4 Estado de equilibrio final
Tras cerrar el interruptor, el conductor 2 se conecta a tierra a través de una resistencia. Circula una corriente debido a la diferencia de potencial, que desaparece cuando se igualan los potenciales de los extremos. Puesto que la caja permanece a tierra el estado final se caracteriza porque
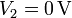
El conductor 2 deja de estar descargado, ya que como consecuencia de la corriente, se ha almacenado una cierta carga en él. El conductor 1, que sigue aislado, mantiene la misma carga que antes
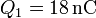
Llevando esto al sistema de ecuaciones anterior nos queda
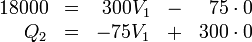
cuya solución es inmediata
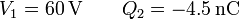
Desde el punto de vista del circuito equivalente, lo que hemos hecho es cortocircuitar el condensador 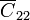 , apareciendo una carga en el condensador
, apareciendo una carga en el condensador 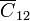 , esto es, que la carga Q2 se almacena en la cara enfrentada al otro bloque.
, esto es, que la carga Q2 se almacena en la cara enfrentada al otro bloque.
La nueva energía vale
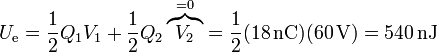
Durante el periodo transitorio se ha disipado una energía

La carga almacenada ahora en la caja también cambia
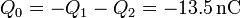
5 Transitorio
Durante el periodo transitorio, esta fluyendo carga a través del cable desde la jaula de Faraday hasta el conductor 2. Por tanto, durante este tiempo la carga del conductor es variable, y también lo es su potencial (ya que la d.d.p. va disminuyendo hasta desaparecer cuando se alcanza de nuevo el equilibrio electrostático). El sistema de ecuaciones anterior debe escribirse
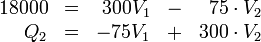
donde las tres incógnitas son funciones del tiempo (el potencial del conductor 1 también se ve afectado al acumularse carga en el 2). Para completar este sistema necesitamos una tercera ecuación. Esta la sacamos de la ley de conservación de la carga. Por tratarse de un dieléctrico ideal, toda la corriente que llega al conductor 2 se emplea en variar la carga almacenada en él

La corriente nos la da la ley de Ohm
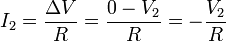
Si expresamos la resistencia en ohmios y la corriente en amperios (con lo que al estar la carga en pC, nos da que el tiempo va en picosegundos), nos queda como tercera ecuación
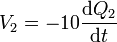
Para resolver el sistema podemos despejar y sustituir, de forma que nos quede una sola ecuación diferencial, que será de coeficientes constantes.
Podemos simplificar el cálculo proponiendo directamente su solución. para ello observamos que la corriente que llega al conductor 2 va a decaer exponencialmente hasta alcanzar el equilibrio electrostático
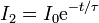
siendo I0 la corriente inmediatamente después de cerrar el interruptor

El signo negativo indica que la corriente en realidad sale del electrodo, pero ello no afecta al cálculo. Por tanto nos queda

con τ el tiempo de relajación que debemos determinar. Ello lo hacemos sustituyendo en el sistema de ecuaciones para cargas, tensiones y corrientes.
De la ley de Ohm queda, para la tensión del conductor 2 en voltios
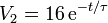
que nos dice, que, como ya sabemos, la tensión del conductor 2 pasa de valer 16 V a anularse cuando se llega al equilibrio electrostático.
De la primera obtenemos para V1
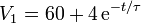
que nos dice, como también sabemos, que el voltaje del conductor 1 pasa de 64 V a 60 V.
Sustituyendo ahora los dos voltajes en la segunda ecuación nos queda la carga en picoculombios
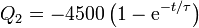
esto es, el conductor 2 inicialmente está descargado y que progresivamente se acumula una carga de -4.5 nC.
Por último, sustituyendo en la ley de conservación de la carga nos resulta
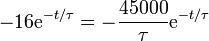
Despejando el tiempo de relajación
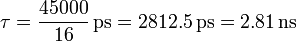
Aun sin haber resuelto exactamente el sistema, es fácil estimar que el tiempo de relajación es del orden del nanosegundo, ya que será del orden de RC, con 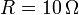 y la capacidades en el rango de los centenares de picofaradios.
y la capacidades en el rango de los centenares de picofaradios.
La potencia disipada en la resistencia, de acuerdo con la ley de Joule
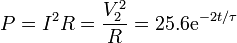
nos da una energía total disipada, en picojulios
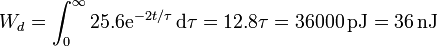
que coincide con la diferencia en la energía almacenada, ya que en este caso no hay aporte externo alguno.





