6.10. Engranaje concéntrico

De Laplace

Revisión a fecha de 19:30 4 sep 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Velocidades angulares
3 Movimiento {34}

1 Enunciado

Se tiene un engranaje formado por un eje central sobre el cual va montado un disco de radio $a$ (sólido “2”) y un anillo exterior estacionario (sólido “1”), de radio $b$ . Entre el disco central y el anillo exterior se encuentra un sistema de dos discos iguales (“3”) y (“4”) que ruedan sin deslizar sobre ambas superficies. Los centros de estos discos se encuentran unidos por una barra articulada “5”. En un momento dado, el disco central se encuentra girando con velocidad angular $Ω$ respecto al anillo fijo exterior y los centros de los discos 3 y 4 se encuentran sobre el eje OX1.

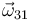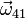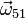Determine las velocidades angulares $\vec{\omega}_{31}$ , $\vec{\omega}_{41}$ y $\vec{\omega}_{51}$ .
¿Qué tipo de movimiento efectúa el disco 3 respecto al 4? ¿Con qué velocidad?

2 Velocidades angulares

2.1 Movimiento {31}

Podemos hallar la velocidad angular en el movimiento {31} a partir de la velocidad lineal de dos puntos del sólido “3” en este movimiento.

Lo más sencillo es tomar como uno de ellos el centro instantáneo de rotación. Puesto que se nos dice que el disco 3 rueda sin deslizar sobre el anillo exterior 1, el CIR $I 31$ no es otro que el punto de contacto del disco con el anillo. Empleando un sistema cartesiano centrado en el sistema

$\overrightarrow{OI}_{31}=b\vec{\imath}\qquad \vec{v}^{I_{31}}_{31}=\vec{0}$

Consideremos ahora el punto A de contacto entre el disco 2 y el 3. Este punto tiene una posición relativa respecto al CIR {31}

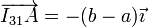
$\overrightarrow{I_{31}A}=-(b-a)\vec{\imath}$

Puesto que se nos dice que el disco 3 también rueda sin deslizar sobre el 2, se cumple

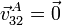
$\vec{v}^A_{32} = \vec{0}$

y por tanto

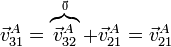
$\vec{v}^{A}_{31} = \overbrace{\vec{v}^A_{32}}^{_\vec{0}}+\vec{v}^A_{21} = \vec{v}^A_{21}$

La velocidad lineal de A en el movimiento 21 es una rotación alrededor del centro del sistema

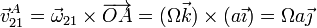
$\vec{v}^A_{21}=\vec{\omega}_{21}\times\overrightarrow{OA}=(\Omega\vec{k})\times(a\vec{\imath}) = \Omega a \vec{\jmath}$

Por tanto

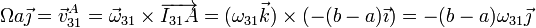
$\Omega a\vec{\jmath}= \vec{v}^A_{31}=\vec{\omega}_{31}\times\overrightarrow{I_{31}A}=(\omega_{31}\vec{k})\times(-(b-a)\vec{\imath})=-(b-a)\omega_{31}\vec{\jmath}$

Igualando componentes, despejamos la velocidad angular

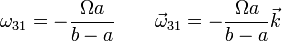
$\omega_{31}=-\frac{\Omega a}{b-a}\qquad\vec{\omega}_{31}=-\frac{\Omega a}{b-a}\vec{k}$

Obsérvese que el disco 3 gira en sentido opuesto al 3. Aunque su centro se mueva describiendo una circunferencia en torno al centro del sistema en sentido antihorario, su rotación alrededor de sí mismo es en sentido horario (respecto a unos ejes fijos ligados al sólido 1).

2.2 Movimiento {41}

El cálculo de la velocidad angular del movimiento {41} es completamente análogo.

El CIR del movimiento {41} es de nuevo el punto de contacto del disco con el anillo exterior

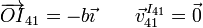
$\overrightarrow{OI}_{41}=-b\vec{\imath}\qquad \vec{v}^{I_{41}}_{41}=\vec{0}$

Consideramos ahora el punto B de contacto entre el disco 2 y el 4. Su posición relativa respecto al CIR {41}

$\overrightarrow{I_{41}B}=(b-a)\vec{\imath}$

El disco 4 también rueda sin deslizar sobre el 2, por lo que se cumple

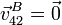
$\vec{v}^B_{42} = \vec{0}$

y por tanto

$\vec{v}^{B}_{41} = \overbrace{\vec{v}^B_{42}}^{_\vec{0}}+\vec{v}^B_{21} = \vec{v}^b_{21}$

La velocidad lineal de B en el movimiento 21 es, como en A, una rotación alrededor del centro del sistema

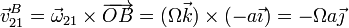
$\vec{v}^B_{21}=\vec{\omega}_{21}\times\overrightarrow{OB}=(\Omega\vec{k})\times(-a\vec{\imath}) = -\Omega a \vec{\jmath}$

Por tanto

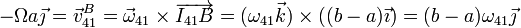
$-\Omega a\vec{\jmath}= \vec{v}^B_{41}=\vec{\omega}_{41}\times\overrightarrow{I_{41}B}=(\omega_{41}\vec{k})\times((b-a)\vec{\imath})=(b-a)\omega_{41}\vec{\jmath}$

Obtenemos la nueva velocidad angular

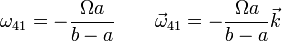
$\omega_{41}=-\frac{\Omega a}{b-a}\qquad\vec{\omega}_{41}=-\frac{\Omega a}{b-a}\vec{k}$

Vemos que el disco 4 gira con la misma velocidad angular que el 3.

6.10. Engranaje concéntrico

De Laplace

Contenido

1 Enunciado

2 Velocidades angulares

2.1 Movimiento {31}

2.2 Movimiento {41}

2.3 Movimiento {51}

3 Movimiento {34}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES