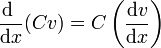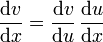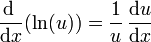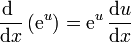Tabla de derivadas y primitivas
De Laplace
Revisión a fecha de 16:54 30 ago 2011; Antonio (Discusión | contribuciones)
Contenido |
1 Reglas de derivación
- Suma de funciones
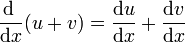
- Producto de funciones
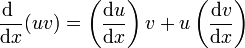
Caso particular u = C = cte
- Regla de la cadena
Caso particular de derivada logarítmica
Caso particular de exponencial de una función
2 Tabla de derivadas
| f(x) | df / dx | f(x) | df / dx |
|---|---|---|---|

| 
| 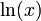
| 
|

| 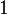
| 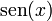
| 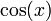
|
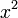
| 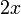
| 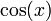
| 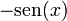
|

| 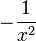
| 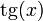
| 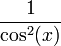
|
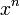
| 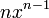
| 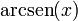
| 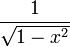
|
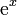
| 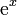
| 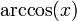
| 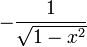
|

| 
| 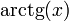
| 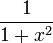
|
3 Tabla de primitivas
| f(x) | 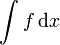
| f(x) | 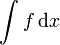
|
|---|---|---|---|

| 
| 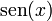
| 
|

| 
| 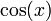
| 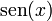
|

| 
| 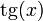
| 
|
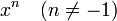
| 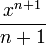
| 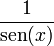
| 
|
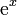
| 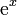
| 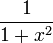
| 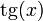
|
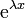
| 
| 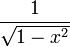
| 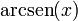
|
Más integrales en la Wikipedia