Acelerómetro eléctrico

De Laplace

Revisión a fecha de 10:52 3 jul 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Variación en la d.d.p.
3 Carga y energía
- 3.1 Carga
- 3.2 Energía

1 Enunciado

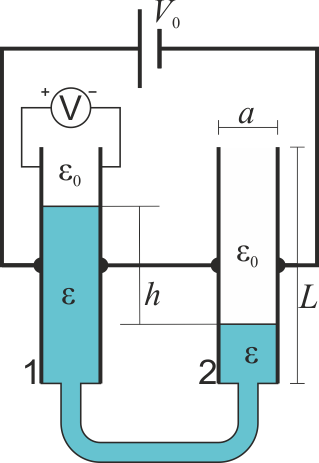
Se construye un acelerómetro eléctrico mediante dos condensadores en serie, de sección cuadrada de lado $L$ y con placas separadas una distancia $a$. Entre los extremos de la asociación se encuentra aplicada una d.d.p. constante $V 0$ . Un líquido dieléctrico ideal, de permitividad $\varepsilon$ , puede pasar de uno a otro condensador. En el estado de movimiento uniforme, el líquido llena hasta la mitad ambos condensadores. Cuando el sistema posee una cierta aceleración, los niveles cambian, de forma que entre los dos condensadores existe un desnivel $h$ (ver figura) relacionado con la aceleración por la ecuación $a / g = h / d$ , siendo d la distancia entre los condensadores.

Halle la diferencia de potencial entre las placas del condensador 1. Calcule la diferencia con su valor para $h = 0$ y, a partir de aquí, obtenga la aceleración del dispositivo.
¿Cuánto varía la carga del condensador 1 cuando el desnivel pasa de $0$ a $h$ ? ¿Y la energía electrostática almacenada en el sistema?

2 Variación en la d.d.p.

Tenemos un sistema formado por dos condensadores, de capacidades $C 1$ y $C 2$ , puestos en serie. Se trata de hallar la diferencia de potencial en uno de ellos, cuando la asociación está sometida a una tensión $V 0$ . Esta d.d.p. es igual a

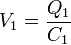
$V_1 = \frac{Q_1}{C_1}$

siendo $Q 1$ la carga del condensador 1, que es la misma que la de la asociación por estar en serie los dos condensadores

Q 1 = Q 2 = Q = C eq V 0

Por tanto, la cantidad que deseamos hallar es

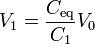
$V_1 = \frac{C_\mathrm{eq}}{C_1}V_0$

La capacidad equivalente de dos condensadores en serie es igual a

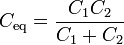
$C_\mathrm{eq} = \frac{C_1C_2}{C_1+C_2}$

por lo que la d.d.p. buscada es

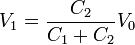
$V_1 = \frac{C_2}{C_1+C_2}V_0$

A su vez, cada una de las capacidades individuales equivale a la de una asociación en paralelo de dos condensadores

$C_1 = C_{1a}+C_{1b}\qquad\qquad C_2 = C_{2a}+C_{2b}$

siendo las capacidades elementales

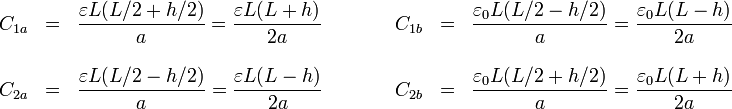
$\begin{array}{rclcrcl} C_{1a} & = & \displaystyle\frac{\varepsilon L(L/2+h/2)}{a} = \frac{\varepsilon L(L+h)}{2a} & \qquad & C_{1b} & = & \displaystyle\frac{\varepsilon_0 L(L/2-h/2)}{a} = \frac{\varepsilon_0 L(L-h)}{2a} \\ & & & & & & \\ C_{2a} & = & \displaystyle\frac{\varepsilon L(L/2-h/2)}{a} = \frac{\varepsilon L(L-h)}{2a} & \qquad & C_{2b} & = & \displaystyle\frac{\varepsilon_0 L(L/2+h/2)}{a} = \frac{\varepsilon_0 L(L+h)}{2a} \end{array}$

y las de los condensadores 1

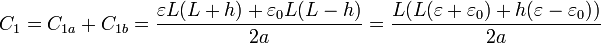
$C_1 = C_{1a}+C_{1b}=\frac{\varepsilon L(L+h)+\varepsilon_0 L(L-h)}{2a}= \frac{L(L(\varepsilon+\varepsilon_0)+h(\varepsilon-\varepsilon_0))}{2a}$

y 2

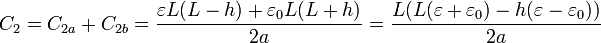
$C_2 = C_{2a}+C_{2b}=\frac{\varepsilon L(L-h)+\varepsilon_0 L(L+h)}{2a}= \frac{L(L(\varepsilon+\varepsilon_0)-h(\varepsilon-\varepsilon_0))}{2a}$

La suma de las dos capacidades es independiente de $h$

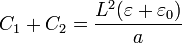
$C_1+C_2 = \frac{L^2(\varepsilon+\varepsilon_0)}{a}$

y la diferencia de potencial en el condensador 1

$V_1 = \frac{C_2}{C_1+C_2}V_0 = \left(\frac{L(L(\varepsilon+\varepsilon_0)-h(\varepsilon-\varepsilon_0))}{2a}\right)\left(\frac{a}{L^2(\varepsilon+\varepsilon_0)}\right)V_0$

Simplificando

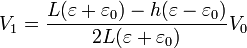
$V_1 = \frac{L(\varepsilon+\varepsilon_0)-h(\varepsilon-\varepsilon_0)}{2L(\varepsilon+\varepsilon_0)}V_0$

Esta es la d.d.p. para cualquier valor de $h$ . Para el caso de aceleración nula $h = 0$ y

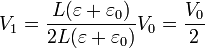
$V_1 = \frac{L(\varepsilon+\varepsilon_0)}{2L(\varepsilon+\varepsilon_0)}V_0= \frac{V_0}{2}$

esto es, cae la mitad de la tensión en cada condensador, como era de esperar.

Obtenemos la variación en la tensión entre $h = 0$ y un valor genérico de h restando

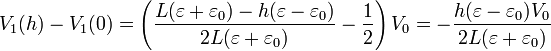
$V_1(h) - V_1(0) = \left(\frac{L(\varepsilon+\varepsilon_0)-h(\varepsilon-\varepsilon_0)}{2L(\varepsilon+\varepsilon_0)}-\frac{1}{2}\right)V_0 = -\frac{h(\varepsilon-\varepsilon_0)V_0}{2L(\varepsilon+\varepsilon_0)}$

La variación es proporcional al desnivel $h$ . De aquí podemos despejar este desnivel

$h = -{2L(\varepsilon+\varepsilon_0)}{(\varepsilon-\varepsilon_0)V_0}(V_1(h)-V_1(0))$

y finalmente obtenemos la aceleración

$a = \frac{gh}{d}=-{2L(\varepsilon+\varepsilon_0)g}{d(\varepsilon-\varepsilon_0)V_0}(V_1(h)-V_1(0))$

3 Carga y energía

3.1 Carga

3.2 Energía

Acelerómetro eléctrico

De Laplace

Contenido

1 Enunciado

2 Variación en la d.d.p.

3 Carga y energía

3.1 Carga

3.2 Energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES