Entrar Página Discusión Historial Go to the site toolbox

Potencial eléctrico fuera de un conductor

De Laplace

Contenido

1 Enunciado

En el exterior de una esfera conductora puesta a tierra se encuentra una cierta densidad de carga eléctrica de forma que el potencial eléctrico en el exterior de la esfera tiene la expresión

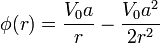
\phi(r) = \frac{V_0a}{r}-\frac{V_0a^2}{2r^2}

y es nulo en su interior.

  1. Determine el radio de la esfera conductora.
  2. Halle el campo eléctrico en todos los puntos del espacio.
  3. Calcule las densidades de carga que son fuentes de este campo.
  4. Halle la carga total de la distribución.
  5. Calcule la energía electrostática almacenada en el sistema.

2 Radio de la esfera

El radio de la esfera lo calculamos sabiendo que éta se encuentra conectada a tierra y por tantu su tensión vale 0. Buscamos entonces en qué punto se anula el potencial

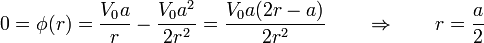
0 = \phi(r) = \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} = \frac{V_0a(2r-a)}{2r^2}\qquad\Rightarrow\qquad r = \frac{a}{2}

Por tanto, la esfera tiene radio a / 2 y la distribución del potencial es

\phi(r) = \begin{cases} 0 & r < \displaystyle\frac{a}{2} \\ & \\ \displaystyle \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} & r > \displaystyle \frac{r}{2}\end{cases}

3 Campo eléctrico

4 Densidades de carga

4.1 Volumétrica

4.2 Superficial

5 Carga total

6 Energía electrostática

6.1 A partir del potencial

6.2 A partir del campo

Obtenido de "http://tesla.us.es/wiki/index.php/Potencial_el%C3%A9ctrico_fuera_de_un_conductor"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace