Amperímetro de inducción

De Laplace

Revisión a fecha de 20:39 24 jun 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

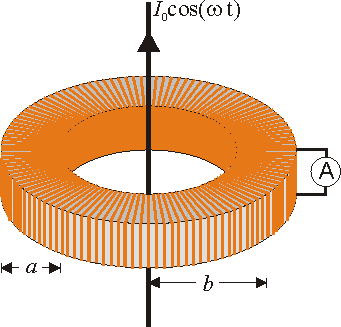
Un amperímetro de inducción consiste en un solenoide toroidal (de resistencia despreciable y autoinducción $L\,$ ), que se sitúa en torno a la corriente que se pretende medir.

Suponga un toroide de radio medio $b$ y sección cuadrada pequeña de lado $a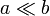$ ( $a\ll b$ ), con $N$ espiras arrolladas sobre un núcleo de permeabilidad $μ$ (en este problema, ello solo supone cambiar $μ 0$ por $μ$ ). Calcule el coeficiente de autoinducción de este solenoide, a partir del campo que se crea en su interior cuando por el solenoide circula una corriente $I$ . 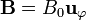Suponga que dentro del solenoide $\mathbf{B}$ es de la forma $\mathbf{B}=B_0\mathbf{u}_{\varphi}$ con $B 0$ uniforme.
El solenoide anterior se coloca concéntricamente con un hilo rectilíneo por el cual circula una corriente $I 0 cos(ω t)$ . Calcule la fuerza electromotriz que el hilo induce en el solenoide.
Despreciando la resistencia del solenoide (pero no su autoinducción), hállese la amplitud de la corriente que circula por el solenoide.
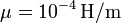Esta amplitud es proporcional a la de la corriente del hilo, ¿cuánto vale la constante de proporcionalidad para un toroide de radio medio 2cm, y lado 2mm, con 300 espiras y con un núcleo de permeabilidad $\mu=10^{-4}\,\mathrm{H}/\mathrm{m}$ ?

2 Solución

2.1 Cálculo de L

La corriente que circula por la superficie del toroide produce un campo acimutal, cuyo módulo es prácticamente uniforme en el interior del toroide (debido a la pequeñez de la sección). Podemos determinar este campo a partir de la ley de Ampère.

Tomando un contorno circular por el interior del toroide, la circulación del campo magnético vale

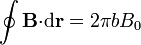
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = 2\pi b B_0$

(ya que el radio de la circunferencia se puede tomar igual al radio medio). Esta circulación debe ser igual a $μ$ , la permeabilidad del material, multiplicada por la corriente total que atraviesa una superficie apoyada en la circunferencia. Esta corriente total vale $I$ (la corriente que va por el solenoide) multiplicada por $N$ , el número de espiras, ya que todas ellas atraviesan el círculo de radio $b$ . Por tanto

$2\pi b B_0 = \mu N I\,$

y el campo en el interior del material vale

$\mathbf{B} = \frac{\mu N I}{2\pi b}\mathbf{u}_{\varphi}$

Para calcular el coeficiente de autoinducción necesitamos el flujo de este campo a través del propio solenoide. Dado que este campo atraviesa las secciones de todas las espiras, tendremos

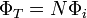
$\Phi_T = N \Phi_i\,$

siendo el flujo individual aproximadamente igual al producto del campo por la sección de cada espira (de nuevo, porque el campo es casi uniforme; si la sección no fuera pequeña sería necesario hallar la integral). Según esto

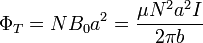
$\Phi_T = N B_0 a^2 = \frac{\mu N^2 a^2 I}{2\pi b}$

y de aquí el coeficiente de autoinducción

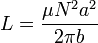
$L = \frac{\mu N^2 a^2}{2\pi b}$

Este coeficiente responde a la forma 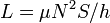$L = \mu N^2 S/h\,$ de un solenoide recto, ya que al ser de pequeña sección los efectos de curvatura son despreciables (similarmente a como ocurre en un conductor filiforme).

2.2 Cálculo de la f.e.m. inducida

La fuerza electromotriz en el solenoide, debida al hilo, valdrá, de acuerdo con la ley de Faraday,

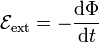
$\mathcal{E}_\mathrm{ext} = -\frac{\mathrm{d}\Phi}{\mathrm{d}t}$

siendo 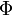$\Phi\,$ el flujo del campo debido al hilo. El campo magnético producido por un hilo infinito vale, en el vacío,

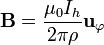
$\mathbf{B} = \frac{\mu_0 I_h}{2\pi \rho}\mathbf{u}_{\varphi}$

En el material, que tiene permeabilidad $μ$ y radio $b$ este campo se convierte en

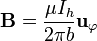
$\mathbf{B} = \frac{\mu I_h}{2\pi b}\mathbf{u}_{\varphi}$

El flujo de este campo a través del solenoide es absolutamente análogo al del apartado anterior.

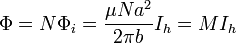
$\Phi = N \Phi_i = \frac{\mu N a^2}{2\pi b} I_h = M I_h$

Obsérvese que la única diferencia se encuentra en el factor 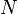$N\,$ que en el coeficiente de autoinducción aparece como $N^2\,$ .

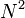La fuerza electromotriz inducida vale

$\mathcal{E}_\mathrm{ext} = -\frac{\mathrm{d}\Phi}{\mathrm{d}t}= -M \frac{\mathrm{d}I_h}{\mathrm{d}t} = M\omega I_0 \,\mathrm{sen}(\omega t)$

2.3 Corriente inducida en el solenoide

La corriente que circula por el solenoide cumplirá la ecuación

$L\frac{\mathrm{d}I}{\mathrm{d}t} = \mathcal{E}_\mathrm{ext} = M\omega I_0\,\mathrm{sen}(\omega t)$

La integración de esta ecuación es inmediata

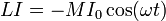
$L I = - M I_0 \cos(\omega t)\,$

y la corriente que circula por la bobina es

$I = - \frac{M}{L} I_0 \cos(\omega t)\,$

Sustituyendo las expresiones para $M$ y $L$ el resultado es simplemente

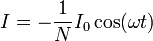
$I = -\frac{1}{N} I_0\cos(\omega t)$

La amplitud de la corriente alterna inducida resulta ser igual a la que circula por el hilo, dividida por el número de espiras. Los demás parámetros son indiferentes.

2.4 Cálculo de la constante de proporcionalidad

Para el caso numérico proporcionado la constante de proporcionalidad es simplemente

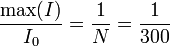
$\frac{\mathrm{max}(I)}{I_0} = \frac{1}{N} = \frac{1}{300}$

esto es, circula una corriente 300 veces menor por el solenoide que por el hilo, lo que la hace más fácilmente medible.

Puede entonces plantearse por qué es necesario el núcleo de material. La razón es que si $μ$ es grande el resultado anterior sigue siendo cierto incluso si el solenoide no es concéntrico con el hilo, lo que hace mucho más fácil el proceso de medida.

Amperímetro de inducción

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Cálculo de L

2.2 Cálculo de la f.e.m. inducida

2.3 Corriente inducida en el solenoide

2.4 Cálculo de la constante de proporcionalidad

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES