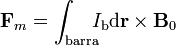Espira con barra deslizante y generador real

De Laplace

Revisión a fecha de 16:17 24 jun 2011; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Fuerzas electromotrices e intensidades de corriente
- 2.2 Fuerzas sobre la barra móvil

1 Enunciado

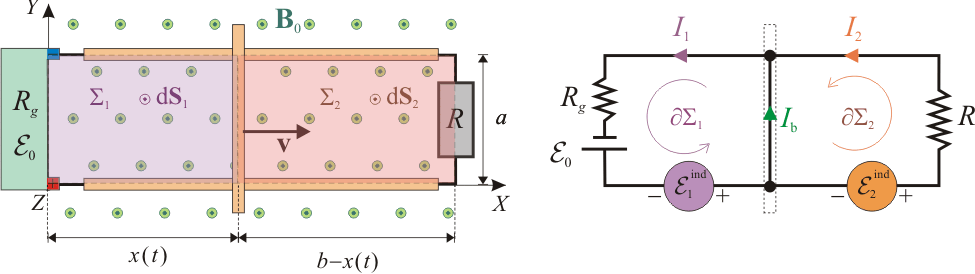
Una espira plana rectangular de autoinducción despreciable está formada por dos raíles perfectamente conductores de longitud

b

, separados una distancia

a

. Los raíles están conectados por uno de sus extremos a una resistencia eléctrica de valor

R

(resistencia de carga) y por el otro a un generador real de fuerza electromotriz constante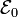 $\mathcal{E}_0$ y resistencia interna

R g

, según se muestra en la figura. Además, una barra perfectamente conductora se mueve con velocidad constante $\mathbf{v}$ , manteniéndose siempre en contacto con los raíles y perpendicular a ellos. La espira se encuentra sometida a un campo magnético constante y uniforme $\mathbf{B}_0$ , perpendicular al plano que contiene a la espira.

Obtenga las fuerzas electromotrices totales en cada malla del circuito y las intensidades de corriente eléctrica que recorren las diferentes ramas.
Calcule la fuerza magnética ejercida sobre la barra móvil, así como la fuerza exterior que se la ha de aplicar para que se mueva según las condiciones del enunciado. Describa la dependencia del sentido de esta fuerza con la velocidad y el sentido de movimiento de la barra.
Realice un balance energético en el sistema: calcule la potencia disipada por efecto Joule en la resistencia de carga, la potencia suministrada por el generador real al resto del sistema y el trabajo que por unidad de tiempo realiza la fuerza externa (potencia mecánica).
La potencia eléctrica suministrada por el generador real y la potencia mecánica realizada por la fuerza exterior, ¿son siempre positivas? Analice cómo depende el signo de éstas de la rapidez y sentido de movimiento de la barra y explique en cada caso dónde se produce y dónde se absorbe la energía en el sistema.

2 Solución

Adoptamos un sistema de referencia cartesiano cuyas direcciones $X$ y $Z$ van a estar definidas, respectivamente, por la dirección de movimiento de la barra conductora y por la dirección del campo magnético uniforme. Es decir,

$\mathbf{v}=v \mathbf{u}_x\ \mathrm{;}\qquad \mathbf{B}_0=B_0 \mathbf{u}_z$

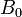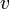En el enunciado se indica que tanto $\displaystyle B_0$ como $\displaystyle v$ , van a ser valores constantes. Por otra parte, podemos considerar sin pérdida de generalidad que 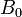$\displaystyle B_0$ es una cantidad positiva (el sentido del eje $O X$ es el del campo magnético); sin embargo, la celeridad 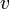$\displaystyle v$ va a ser es un número real cuyo signo indica el sentido de movimiento de la barra conductora.

2.1 Fuerzas electromotrices e intensidades de corriente

Obsérvese que el flujo magnético del campo $\mathbf{B}_0$ a través de la espira formada por los dos raíles, la resistencia de carga $R$ y el generador, es constante en el tiempo ya que, tanto dicha espira como el campo magnético no cambian el tiempo y, además, este último es uniforme. En consecuencia, el valor neto de la fuerza electromotriz inducida en la espira es nula. 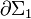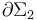Sin embargo, la barra conductora móvil determina sendos circuitos, $\partial \Sigma_1$ y $\partial\Sigma_2$ , ambos de sección variable. Calculemos el flujo magnético a través de cada uno de ellos, tomando los diferenciales de superficie en todos sus puntos con la dirección y sentido del campo magnético:

$\mathrm{d} \mathbf{S}_1=\mathrm{d} \mathbf{S}_2=\mathrm{d}S\ \mathbf{u}_z\;\;\Longrightarrow\;\;\left\{\begin{array}{l}\displaystyle \Phi_m\rfloor_{\Sigma_1}=\int_{\Sigma_1}\!\!\mathbf{B}_0\cdot\mathrm{d} \mathbf{S}_1=B_0\int_{\Sigma_1}\!\!\mathrm{d}S =B_0 a x(t) \\ \\ \displaystyle\Phi_m\rfloor_{\Sigma_2}=\int_{\Sigma_2}\!\!\mathbf{B}_0\cdot\mathrm{d} \mathbf{S}_2=B_0\int_{\Sigma_2}\!\!\mathrm{d}S=B_0 a [b-x(t)] \end{array}\right.$

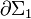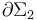Como puede comprobarse, ambos son funciones del tiempo al serlo también la variable geométrica $x (t)$ que indica la posición de la barra móvil a lo largo del tiempo. Según la ley de Faraday, el cambio temporal de dichos flujos da lugar a la aparición de sendas fuerzas electromotrices inducidas en los circuitos $\partial \Sigma_1$ y $\partial\Sigma_2$ :

$\begin{array}{l}\displaystyle\mathcal{E}_1^\mathrm{ind}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}\bigg\rfloor_{\Sigma_1}=-B_0 a\ \frac{\mathrm{d}x(t)}{\mathrm{d}t}=-B_0 a v\\ \\ \displaystyle\mathcal{E}_2^\mathrm{ind}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t} \bigg\rfloor_{\Sigma_2}=-B_0 a\ \frac{\mathrm{d}}{\mathrm{d}t}\big[b-x(t)\big]=B_0 a v\end{array}$

En las expresiones anteriores se ha tenido en cuenta que la derivada temporal de la variable $x (t)$ es, precisamente, la celeridad $v$ que caracteriza al movimiento rectilíneo uniforme de la barra. Nótese que estas f.e.m. inducidas son opuestas, lo cual es coherente con la consideración inicial de que la f.e.m. neta inducida en la espira (sin la barra móvil), debe ser nula.

Por otra parte, tal como se muestra en el circuito equivalente de la siguiente figura, el sentido de estas fuerzas electromotrices ha de ser consistente con el sentido propuesto para la intensidad de corriente que recorre cada circuito que, a su vez, está determinado por el sentido adoptado para los diferenciales de superficie en $Σ 1$ y $Σ 2$ .

Obsérvese que en el circuito 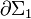$\partial\Sigma_1$ , dicho sentido coincide con el determinado por la fuerza electromotriz 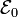$\mathcal{E}_0$ del generador real. Por tanto, la fuerza electromotriz total en esta malla es igual a la suma de aquélla y de la inducida; por otra parte, aplicando la segunda ley de Kirchoff obtenemos la ecuación del circuito para esta malla:

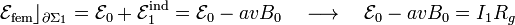
$\mathcal{E}_\mathrm{fem}\rfloor_{\partial \Sigma_1}=\mathcal{E}_0+\mathcal{E}_1^\mathrm{ind}=\mathcal{E}_0-avB_0\quad\longrightarrow\quad \mathcal{E}_0-avB_0=I_1 R_g$

\noindent pues toda la caída de tensión se producirá en la resistencia interna del generador, ya que los raíles y la barra móvil se consideran conductores perfectos.

El circuito 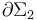$\partial\Sigma_2$ está constituido por dichos medios conductores y la resistencia de carga $R$ . La única f.e.m. es la inducida, teniéndose, por tanto,

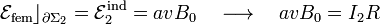
$\mathcal{E}_\mathrm{fem}\rfloor_{\partial \Sigma_2}=\mathcal{E}_2^\mathrm{ind}=avB_0\quad\longrightarrow\quad avB_0=I_2 R$

Las anteriores ecuaciones permiten determinar las intensidades de corriente en las ramas del sistema. Las respectivas intensidades de corriente eléctrica que recorren el generador real y la resistencia de carga son,

$I_1=\frac{\mathcal{E}_0-avB_0}{R_g}\ \mathrm{;}\qquad I_2=\frac{avB_0}{R}$

de manera que el valor y el signo de $v$ van a determinar el sentido de ambas corrientes: la intensidad $I 2$ que recorre la resistencia de carga será positiva (según el sentido prefijado) si la barra se mueve hacia la resistencia de carga, y negativa si se desplaza hacia el generador. Por su parte, la corriente $I 1$ será positiva o negativa dependiendo de que la velocidad de la barra sea menor o mayor, respectivamente, que el valor crítico,

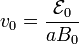
$v_0=\frac{\mathcal{E}_0}{aB_0}$

Para determinar la intensidad de corriente eléctrica $I b$ que recorre la barra conductora aplicamos la primera ley de Kirchoff en el nodo correspondiente a uno de los puntos de contacto barra--raíl:

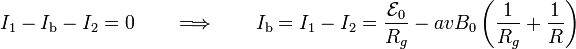
$I_1-I_\mathrm{b}-I_2=0\qquad\Longrightarrow\qquad I_\mathrm{b}=I_1-I_2=\frac{\mathcal{E}_0}{R_g}-avB_0\left(\frac{1}{R_g}+\frac{1}{R}\right)$

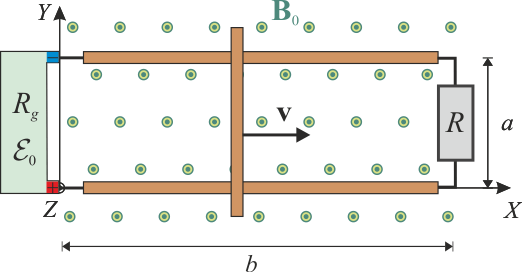
2.2 Fuerzas sobre la barra móvil

Acabamos de comprobar que, cuando se mueve en contacto con los raíles, la barra es recorrida por una corriente eléctrica cuya intensidad

I b

depende (entre otros parámetros) de la rapidez del movimiento. Y como la barra conductora está sometida al campo magnético $\mathbf{B}_0$ , éste ejercerá sobre ella una fuerza magnética

$\mathbf{F}_m=\int_\mathrm{barra}\!\!\!I_\mathrm{b}\mathrm{d}\mathbf{r}\times\mathbf{B}_0$

Espira con barra deslizante y generador real

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas electromotrices e intensidades de corriente

2.2 Fuerzas sobre la barra móvil

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES