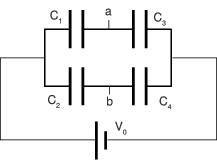Cuatro condensadores Primera Prueba de Control 2010/11 (F2GIA)
De Laplace
1 Enunciado
En el circuito de la figura, ¿cuál es la relación más general que debe cumplirse entre las capacidades de los cuatro condensadores para que los puntos a y b estén al mismo potencial?
-
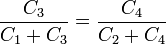 .
.
- C1 = C2 y C3 = C4.
- C1 = C3 y C2 = C4.
-
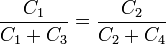 .
.
2 Solución
La respuesta correcta es la 1
Para que el potencial en a y b sea el mismo la diferencia de potencial en los condensadores 1 y 2 debe ser la misma. Entonces
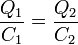
Por otro lado, la caída de tensión a lo largo de los condensadores 1 y 3 debe ser V0, así como la caída de tensión a lo largo de los condensadores 2 y 4. Ahora bien, los condensadores 1 y 3 están en serie, por lo que
Q1 = Q3
Asimismo, los condensadores 2 y 4 también están en serie, por lo que
Q2 = Q4
Calculando la caída de tensión a través de 1 y 3, y a través de 2 y 4 obtenemos
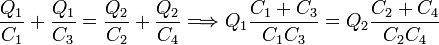
Dividiendo esta igualdad por la primera obtenida vemos que debe cumplirse
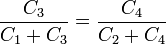
Hay que señalar que las opciones 2 y 3 del test también dan el mismo potencial en los puntos a y b. Sin embargo, ninguna de las dos es la relación más general. Si se cumple la opción 2 o la 3 se cumple la 1. Pero si se cumple la 1 no tienen por qué cumplirse la 2 o la 3.