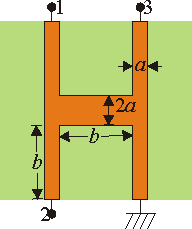
Pista en forma de H

De Laplace

Revisión a fecha de 11:33 13 mar 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Coeficientes de conductancia
3 Circuito equivalente
4 Potencia consumida
5 Cambio en la potencia
- 5.1 Empleando el álgebra matricial

1 Enunciado

Se tiene un circuito impreso en forma de "H" de un material de conductividad

σ

, con cuatro terminales, una de las cuales se encuentra permanentemente a tierra. Los brazos de la H y el tabique central poseen longitud

b

. Los cuatro brazos tienen anchura

a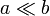

, ( $a\ll b$ ) mientras que el tramo central posee anchura

2 a

, según indica la figura. El espesor de toda la pista es

c

.

Determine la matriz de los coeficientes de conductancia, $G i j$ , correspondiente a los tres terminales libres. Desprecie la pequeña contribución de las esquinas donde confluyen los brazos.
A partir de la matriz anterior, calcule las conductancias 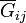$\overline{G}_{ij}$ y elabore un circuito equivalente al sistema de tres electrodos, que no emplee nodos intermedios.
Determine la potencia consumida en la pista cuando el terminal 1 se encuentra a potencial $V 0$ y los otros a tierra.
En la configuración anterior se corta la conexión a tierra del electrodo 2. En el nuevo estado estacionario, ¿se consume más o menos potencia que antes de la desconexión? ¿Cuánto?

2 Coeficientes de conductancia

2.1 Aproximación de conductores filiformes

Puesto que la longitud de las barras es muy superior a su anchura, es una aproximación razonable el tratar cada una de ellas como un conductor filiforme, de longitud $b$ y sección transversal $a c$ en las barras laterales y $2 a c$ en la central.

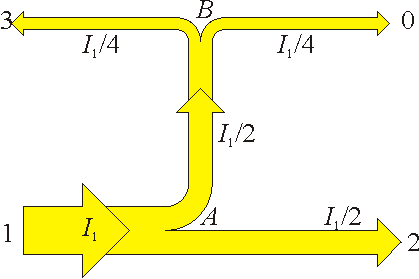
Podemos aproximar entonces el sistema mediante un circuito equivalente formado por cinco resistores conectados en dos nodos centrales, que etiquetaremos como “A” y “B”.

Este circuito equivalente no es, no obstante, el mínimo posible. Más adelante veremos como se puede construir uno que no requiera nodos adicionales.

Los valores de las resistencias de las patas son todas iguales entre sí y a

$R_0= \frac{b}{\sigma a c}$

mientras que la barra central, de doble anchura, tiene resistencia la mitad de esta

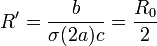
$R' = \frac{b}{\sigma(2a) c} = \frac{R_0}{2}$

Puede argumentarse que una mejor aproximación a la longitud de estos conductores sería $(b + a / 2)$ para las barras laterales y $(b + a)$ para la central. Siempre que estemos en la aproximación 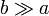$b\gg a$ esta corrección es despreciable. Al final veremos cuánto mejoraría el resultado al incluirla.

Para hallar los coeficientes de conductancia podemos hacerlo de dos formas:

Suponer sucesivamente cada uno de los electrodos a potencial $V 0$ y hallar la corriente que entra por cada uno. De esta forma calculamos una a una las columnas de la matriz de coeficientes de conductancia.

Suponer simultáneamente tensiones diferentes $V i$ en los distintos electrodos y hallar la corriente que entra por cada uno. Así se halla matriz completa de una sola operación, pero de manera más complicada que en la anterior.

2.2 Fijando tensiones sucesivamente

Suponemos entonces el electrodo 1 a potencial $V 0$ y los otros dos y el de referencia a tierra. Para hallar la corriente que entra por el electrodo 1 podemos hallar la resistencia equivalente del circuito en esta configuración.

Observemos que el electrodo 3 y el de referencia 0 están ambos a tierra. Por ello el resistor que conecta el nodo B y el electrodo 3 se encuentra en paralelo con el que une a B con el 0. La resistencia equivalente de este par cumple

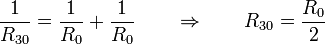
$\frac{1}{R_{30}} = \frac{1}{R_0}+\frac{1}{R_0}\qquad\Rightarrow\qquad R_{30}=\frac{R_0}{2}$

Esta asociación se encuentra en serie con la de la barra central, lo que da la resistencia equivalente

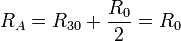
$R_{A}=R_{30}+\frac{R_0}{2}=R_0$

A su vez, esta asociación de tres, está en paralelo con la que une a A con el electrodo 2, por lo que

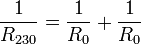
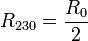
$\frac{1}{R_{230}}=\frac{1}{R_0}+\frac{1}{R_0}$ $\Rightarrow$ $R_{230}=\frac{R_0}{2}$

Por último, esta resistencia se encuentra en serie con la que une el electrodo 1 a A, lo que nos da la resistencia equivalente del sistema completo

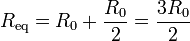
$R_\mathrm{eq} = R_0+\frac{R_0}{2}=\frac{3R_0}{2}$

Por tanto la corriente que entra al electrodo 1 es

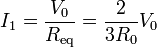
$I_1 = \frac{V_0}{R_\mathrm{eq}}=\frac{2}{3R_0}V_0$

lo que nos da el primer coeficiente de conductancia

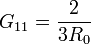
$G_{11}=\frac{2}{3R_0}$

Para hallar el coeficiente $G 21$ necesitamos la corriente que, en esta situación, llega al electrodo 2. Dado que del a partir del nodo A la corriente se reparte entre dos ramas de igual resistencia, la corriente que llega a 2 desde el 1 es la mitad de la anterior. Puesto que tomamos el criterio de signos considerando positivas que van hacia el electrodo desde el exterior obtenemos

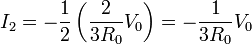
$I_2 = -\frac{1}{2}\left(\frac{2}{3R_0}V_0\right)=-\frac{1}{3R_0}V_0$

lo que nos da el coeficiente

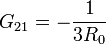
$G_{21}=-\frac{1}{3R_0}$

Para la corriente que llega a 3 observamos que la corriente que llega a B desde A (la mitad de la original) se vuelve a subdividir en dos partes iguales entre el electrodo 3 y el de referencia. Por tanto

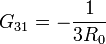
$I_3 = -\frac{1}{4}\left(\frac{2}{3R_0}V_0\right)=-\frac{1}{6R_0}V_0$ $\Rightarrow$ $G_{31}=-\frac{1}{3R_0}$

Ahora deberíamos repetir el proceso suponiendo el electrodo 2 a potencial $V 0$ y el resto a tierra, para calcular la segunda columna. Sin embargo, no es necesario: desde el punto de vista de la geometría del circuito, la situación es idéntica, cambiando solamente las etiquetas de los electrodos (concretamente la 1 por la 2). Así obtenemos

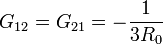
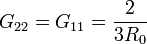
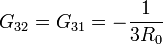
$G_{12} = G_{21}=-\frac{1}{3R_0}$ $G_{22}=G_{11}=\frac{2}{3R_0}$ $G_{32}=G_{31}=-\frac{1}{3R_0}$

Lo mismo ocurre si es el electrodo 3 el que se pone a potencial $V 0$ , por lo que

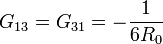
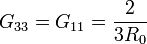
$G_{13} = G_{31}=-\frac{1}{6R_0}$ $G_{23}=G_{32}=-\frac{1}{3R_0}$ $G_{33}=G_{11}=\frac{2}{3R_0}$

Reuniendo todos los resultados en una sola matriz

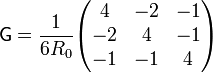
$\mathsf{G}=\frac{1}{6R_0}\begin{pmatrix}4 & -2 & -1 \\ -2 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}$

Vemos que resulta una matriz simétrica en la que los elementos de la diagonal principal son todos positivos, mientras que los no diagonales son negativos.

2.3 Fijando las tensiones simultáneamente

Suponemos ahora el electrodo 1 a potencial $V 1$ , el 2 a $V 2$ y el 3 a $V 3$ y los otros dos y el de referencia a tierra. Si llamamos $V A$ a la tensión del nodo central más próximo al electrodo 1 y $V B$ al más alejado de este electrodo, tenemos las siguientes ecuaciones, por aplicación reiterada de la ley de Ohm

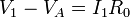
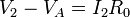
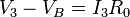
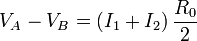
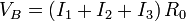
$V_1 - V_A = I_1R_0\,$ $V_2 - V_A = I_2R_0\,$ $V_3 - V_B = I_3R_0\,$ $V_A - V_B = \left(I_1+I_2\right)\frac{R_0}{2}\,$ $V_B = \left(I_1+I_2+I_3\right)R_0\,$

Eliminando V_A y V_B de estas ecuaciones llegamos a

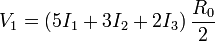
$V_1 = \left(5I_1+3I_2+2I_3\right)\frac{R_0}{2}$ $V_2 = \left(3I_1+5I_2+2I_3\right)\frac{R_0}{2}$ $V_3 = \left(2I_1+2I_2+4I_3\right)\frac{R_0}{2}$

que podemos expresar en forma matricial como

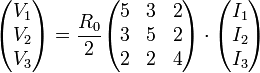
$\begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}=\frac{R_0}{2}\begin{pmatrix}5 & 3 & 2 \\ 3 & 5 & 2 \\ 2 & 2 & 4\end{pmatrix}\cdot\begin{pmatrix}I_1 \\ I_2 \\ I_3\end{pmatrix}$

o, simbólicamente

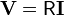
$\mathbf{V}=\mathsf{R}\mathbf{I}\,$

Invirtiendo esta relación matricial llegamos a la matriz de coeficientes de conductancia

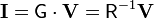
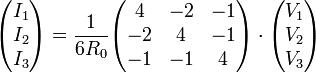
$\mathbf{I}=\mathsf{G}\cdot\mathbf{V}=\mathsf{R}^{-1}\mathbf{V}\,$ $\Rightarrow$ $\begin{pmatrix}I_1 \\ I_2 \\ I_3\end{pmatrix}=\frac{1}{6R_0}\begin{pmatrix}4 & -2 & -1 \\ -2 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot\begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}$

o, separando por coeficientes,

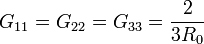
$G_{11}=G_{22}=G_{33}=\frac{2}{3R_0}$ $G_{12}=G_{21}=\frac{1}{3R_0}$ $G_{13}=G_{23}=G_{31}=G_{32}=\frac{1}{6R_0}$

3 Circuito equivalente

Aunque el anterior es un circuito equivalente (de los que hay infinitos posibles), no se trata del circuito equivalente mínimo, que considera exclusivamente las corrientes que van de un electrodo a otro, sin emplear nodos intermedios.

Este circuito mínimo se construye en los siguientes pasos:

Un nodo por cada electrodo “activo” (aquellos cuya tensión es variable; todos menos el de referencia).
Uno nodo adicional, etiquetado como “0” para el electrodo de referencia.
Un resistor entre cada par de nodos activos, cuya conductancia es

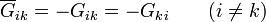
$\overline{G}_{ik}=-G_{ik}=-G_{ki}\qquad (i\neq k)$

en nuestro caso, esto corresponde a

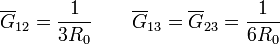
$\overline{G}_{12} = \frac{1}{3R_0}\qquad \overline{G}_{13}=\overline{G}_{23}=\frac{1}{6R_0}$

Un resistor entre cada nodo y el de referencia, con conductancia la suma de la fila (o columna) correspondiente de la matriz

$\overline{G}_{ii}=\sum_k G_{ik}$

que para este caso concreto da

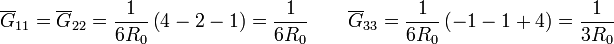
$\overline{G}_{11}=\overline{G}_{22}=\frac{1}{6R_0}\left(4-2-1\right)=\frac{1}{6R_0}\qquad \overline{G}_{33}=\frac{1}{6R_0}\left(-1-1+4\right)=\frac{1}{3R_0}$

Aparte, habría que añadir las fuentes de tensión o de intensidad correspondientes. Puesto que en este caso no se especifica ninguna, dejamos ese aspecto pendienete para cada caso particular.

Observemos que las conductancias resultantes mantienen la simetría geométrica del sistema, dependiendo de si los electrodos están conectados por solo dos tramos o por tres tramos consecutivos.

4 Potencia consumida

La potencia consumida la podemos hallar de diversas formas. La expresión general para la potencia consumida en un sistema óhmico es

P = \sum I i V i i

o, en forma matricial

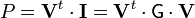
$P=\mathbf{V}^t\cdot \mathbf{I}=\mathbf{V}^t\cdot\mathsf{G}\cdot\mathbf{V}$

una forma inmediata consiste en aplicar esta fórmula a nuestro caso concreto, en el que $V 1 = V 0$ y el resto de las tensiones son nulas

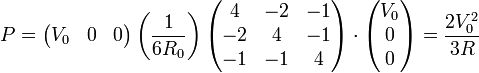
$P=\begin{pmatrix} V_0 & 0 & 0 \end{pmatrix}\left(\frac{1}{6R_0}\right)\begin{pmatrix} 4 & -2 & -1 \\ -2 & 4 & -1 \\ -1 & -1 & 4\end{pmatrix}\cdot\begin{pmatrix} V_0 \\ 0 \\ 0 \end{pmatrix}=\frac{2V_0^2}{3R}$

Una segunda posibilidad consiste en calcular previamente las diferentes intensidades de corriente y luego multiplicar por las tensiones respectivas

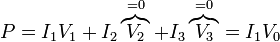
$P = I_1V_1+I_2\overbrace{V_2}^{=0}+I_3\overbrace{V_3}^{=0} = I_1V_0$

Por tanto, solo precisamos la corriente que entra en el electrodo 1 cuando éste se encuentra a potencial $V 0$ y el resto a tierra. Este valor ya lo calculamos antes

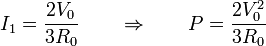
$I_1 = \frac{2V_0}{3R_0}\qquad \Rightarrow\qquad P = \frac{2V_0^2}{3R_0}$

A este valor también se llega directamente con la resistencia equivalente del sistema

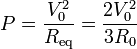
$P = \frac{V_0^2}{R_\mathrm{eq}} = \frac{2V_0^2}{3R_0}$

Otra posibilidad consiste en analizar el circuito equivalente inicial, hallar la corriente que fluye por cada rama y sumar la potencia disipada en cada una de ellas

$P = (I_1)^2 R_0 + \left(\frac{I_1}{2}\right)^2 R_0 + \left(\frac{I_1}{2}\right)^2 \frac{R_0}{2}+\left(\frac{I_1}{4}\right)^2 R_0+\left(\frac{I_1}{4}\right)^2 R_0= I_1^2R_0\left(1+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{16}\right)=\frac{3}{2}I_1^2R_0$

Sustituyendo el valor de la corriente que entra en el electrodo 1 reobtenemos el resultado ya conocido

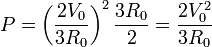
$P = \left(\frac{2V_0}{3R_0}\right)^2\frac{3R_0}{2}= \frac{2V_0^2}{3R_0}$

5 Cambio en la potencia

En el segundo caso, abrimos la conexión del electrodo 2. Esto quiere decir que a partir de ese momento, por ese electrodo ni entra ni sale corriente:

$I_2 = 0\,$

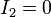
Si aplicamos de nuevo la fórmula de la potencia para un sistema de N electrodos

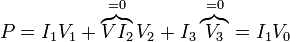
$P = I_1V_1+\overbrace{VçI_2}^{=0}V_2+I_3\overbrace{V_3}^{=0} = I_1V_0$

que parece predecir el mismo resultado que en el apartado anterior. La diferencia reside en que $I 1$ ha cambiado. No sabemos cuanta corriente entra por el electrodo 1 en la nueva situación. Para ello, debemos emplear de nuevo el álgebra matricial o el circuito equivalente.

5.1 Empleando el álgebra matricial

Pista en forma de H

De Laplace

Contenido

1 Enunciado

2 Coeficientes de conductancia

2.1 Aproximación de conductores filiformes

2.2 Fijando tensiones sucesivamente

2.3 Fijando las tensiones simultáneamente

3 Circuito equivalente

4 Potencia consumida

5 Cambio en la potencia

5.1 Empleando el álgebra matricial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

P =	∑	I_iV_i
	i