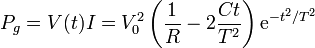Pulso gaussiano de tensión

De Laplace

Revisión a fecha de 18:42 5 mar 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Campo y densidad de corriente
3 Carga e intensidad de corriente
- 3.1 Carga en las placas
- 3.2 Intensidad de corriente
4 Balance energético
5 Energía total disipada

1 Enunciado

Se tiene un condensador con pérdidas formado por dos placas cuadradas de lado 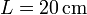$L = 20\,\mathrm{cm}$ , situadas paralelamente a una distancia 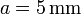$a = 5\,\mathrm{mm}$ . Entre ellas se encuentra un material de permitividad relativa 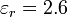$\varepsilon_r = 2.6$ y conductividad 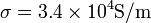$\sigma = 3.4 \times 10^{−4}\mathrm{S}/\mathrm{m}$ . Una placa se encuentra permanentemente a tierra, mientras que la otra experimenta un pulso de tensión de forma gaussiana

$V(t) = V_0\mathrm{e}^{-t^2/T^2}\qquad (-\infty < t < \infty)$

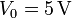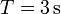con $V_0 = 5\,\mathrm{V}$ y $T = 3\,\mathrm{s}$ .

Para cualquier instante de tiempo, calcule

la distribución de campo eléctrico y de corriente entre las placas. Desprecie los efectos de borde.
la carga en cada una de las placas y la corriente que llega a cada una.
la energía electrostática almacenada, la potencia disipada en el medio, y la potencia desarrollada por el generador.
Calcule igualmente la energía total disipada a lo largo del tiempo, así como el trabajo total realizado por el generador.

Halle el valor numérico de los resultado sélo para el último apartado.

Dato:

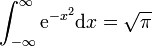
$\int_{-\infty}^{\infty}\mathrm{e}^{-x^2}\mathrm{d}x = \sqrt{\pi}$

2 Campo y densidad de corriente

En principio tenemos un sistema complicado de ecuaciones diferenciales y relaciones constitutivas

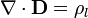
$\nabla\times\mathbf{E}=\mathbf{0}$ $\nabla\cdot\mathbf{D}=\rho_l$ $\nabla\cdot\mathbf{J}=-\frac{\partial \rho_l}{\partial t}$ $\mathbf{D}=\varepsilon \mathbf{E}\qquad\mathbf{J}=\sigma\mathbf{E}$

Sin embargo, por tratarse de un medio homogéneo, se cumple que, si no existe la densidad de carga libre es nula en el instante inicial, también lo es en cualquier otro instante

$\rho_l=0\,$

Por tanto, las ecuaciones se reducen a

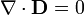
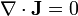
$\nabla\times\mathbf{E}=\mathbf{0}$ $\nabla\cdot\mathbf{D}=0$ $\nabla\cdot\mathbf{J}=0$

que son equivalentes a las de un condensador o una resistencia formada por el material entre dos planos paralelos, siendo su solución

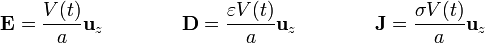
$\mathbf{E}=\frac{V(t)}{a}\mathbf{u}_z\qquad\qquad\mathbf{D}=\frac{\varepsilon V(t)}{a}\mathbf{u}_z\qquad\qquad\mathbf{J}=\frac{\sigma V(t)}{a}\mathbf{u}_z$

3 Carga e intensidad de corriente

3.1 Carga en las placas

Las placas conductoras almacenan cargas de la misma magnitud y signo opuesto. La carga almacenada en la placa a tensión $V (t)$ la hallamos a partir del flujo del vector desplazamiento

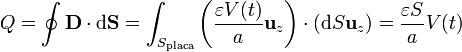
$Q=\oint \mathbf{D}\cdot\mathrm{d}\mathbf{S}=\int_{S_\mathrm{placa}} \left(\frac{\varepsilon V(t)}{a}\mathbf{u}_z\right)\cdot(\mathrm{d}S\mathbf{u}_z)=\frac{\varepsilon S}{a}V(t)$

Esta carga puede también hallarse empleando la capacidad de un condensador.

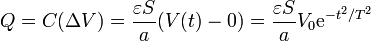
$Q = C(\Delta V)= \frac{\varepsilon S}{a}(V(t)-0) = \frac{\varepsilon S}{a}V_0\mathrm{e}^{-t^2/T^2}$

3.2 Intensidad de corriente

De la ley de conservación de la carga se deduce que la corriente que llega por el cable se emplea en parte en variar la carga almacenada y en parte se escapa a través del material

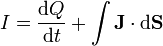
$I = \frac{\mathrm{d}Q}{\mathrm{d}t}+\int \mathbf{J}\cdot\mathrm{d}\mathbf{S}$

El flujo de la densidad de corriente es análogo al del vector desplazamiento calculado en el apartado anterior

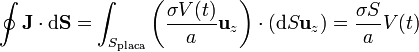
$\oint \mathbf{J}\cdot\mathrm{d}\mathbf{S}=\int_{S_\mathrm{placa}} \left(\frac{\sigma V(t)}{a}\mathbf{u}_z\right)\cdot(\mathrm{d}S\mathbf{u}_z)=\frac{\sigma S}{a}V(t)$

o, en términos de la resistencia o la conductancia del elemento

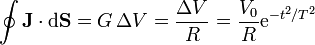
$\oint \mathbf{J}\cdot\mathrm{d}\mathbf{S}=G\,\Delta V = \frac{\Delta V}{R}=\frac{V_0}{R}\mathrm{e}^{-t^2/T^2}$

La variación de la carga almacenada la hallamos derivando el resultado de la sección anterior

$\frac{\mathrm{d}Q}{\mathrm{d}t}=C\frac{\mathrm{d}(\Delta V))}{\mathrm{d}t}=-\frac{CV_0t}{T^2}\mathrm{e}^{-t^2/T^2}$

Sumando los dos términos

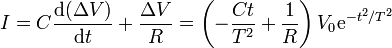
$I = C\frac{\mathrm{d}(\Delta V)}{\mathrm{d}t}+\frac{\Delta V}{R}=\left(-\frac{Ct}{T^2}+\frac{1}{R}\right)V_0\mathrm{e}^{-t^2/T^2}$

4 Balance energético

4.1 Energía almacenada

La energía almacenada es la correspondiente a un condensador

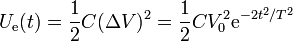
$U_\mathrm{e}(t) = \frac{1}{2}C(\Delta V)^2 = \frac{1}{2}CV_0^2 \mathrm{e}^{-2t^2/T^2}$

4.2 Potencia disipada

La potencia disipada en forma de calor la hallamos empleando la ley de Joule

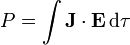
$P = \int \mathbf{J}\cdot\mathbf{E}\,\mathrm{d}\tau$

Teniendo en cuenta que tanto el campo como la densidad de corriente son (aproximadamente) uniformes en el espacio entre las placas, esta integral equivale a

$P = \left(\frac{V(t)}{a}\mathbf{u}_z\right)\cdot\left(\sigma\frac{V(t)}{a}\mathbf{u}_z\right)Sa = \frac{V(t)^2}{a/\sigma S} = \frac{V_0^2}{R}\mathrm{e}^{-2t/\tau}$

4.3 Potencia del generador

El generador desarrolla una potencia instantánea igual al producto de su fuerza electromotriz por la corriente que lo atraviesa

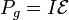
$P_g = I\mathcal{E}$

En este caso, la f.e.m. coincide con la tensión entre las placas y la corriente es la que llega por el cable

$P_g = V(t)I =V_0^2\left(\frac{1}{R}-2\frac{Ct}{T^2}\right)\mathrm{e}^{-t^2/T^2}$

5 Energía total disipada

Pulso gaussiano de tensión

De Laplace

Contenido

1 Enunciado

2 Campo y densidad de corriente

3 Carga e intensidad de corriente

3.1 Carga en las placas

3.2 Intensidad de corriente

4 Balance energético

4.1 Energía almacenada

4.2 Potencia disipada

4.3 Potencia del generador

5 Energía total disipada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES