Entrar Página Discusión Historial Go to the site toolbox

Descarga de un condensador con un medio polarizado

De Laplace

Contenido

1 Enunciado

El sistema de la figura está formado por tres placas conductoras ideales, planas y paralelas, todas de área S. Todas las placas pueden suponerse muy delgadas. Entre la placa “1” y la “2” hay un dieléctrico ideal de espesor a, caracterizado porque presenta una polarización uniforme y constante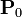 \mathbf{P}_0, perpendicular a dichas placas. Entre las placas “2” y “3”, separadas una distancia b, hay un medio óhmico de conductividad σ y permitividad \varepsilon. Las dos regiones entre las placas están inicialmente descargadas. La placa central se encuentra conectada a un generador, que fija una diferencia de potencial V0 respecto a las otras dos placas, ambas a tierra.
  1. Determine los campos y corrientes en el sistema cuando éste se halla en régimen estacionario.
  2. Calcule las distribuciones estacionarias de carga libre en el sistema. Ajuste el valor de V0 para que la placa central esté descargada. Este valor se usará en los dos apartados siguientes.
  3. En un instante t = 0 se desconecta el generador. Halle la distribución de campos, corrientes y cargas libres en el sistema cuando se alcanza de nuevo una situación estacionaria.
  4. Calcule la evolución en el tiempo de los campos, las corrientes y la carga libre en las placas.

Desprecie los efectos de borde.

2 Solución

2.1 Estado estacionario antes de la desconexión

La clave para resolver este apartado es observar que la placa central es un conductor a potencial fijado y por tanto separa completamente los problemas a un lado y al otro de ella. Así, en lugar de un problema complicado tenemos dos problemas sencillos:

2.1.1 En la región 0 < z < a

Tenemos una región polarizada uniformemente con polarización

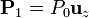
\mathbf{P}_1=P_0\mathbf{u}_z

situada entre dos conductores a potenciales 0 y V0, respectivamente.

Si suponemos despreciables los efectos de borde, dado que el medio entre las placas es homogéneo, el campo eléctrico es uniforme entre las placas y va en la dirección perpendicular a ellas:

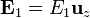
\mathbf{E}_1=E_1\mathbf{u}_z

El valor del campo lo obtenemos de la diferencia de potencial entre las placas:

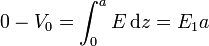
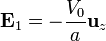
0-V_0=\int_0^a E\,\mathrm{d}z = E_1 a   \Rightarrow   \mathbf{E}_1 = -\frac{V_0}{a}\mathbf{u}_z

y, conocidos el campo y la polarización tenemos el vector desplazamiento:

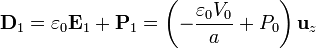
\mathbf{D}_1=\varepsilon_0\mathbf{E}_1+\mathbf{P}_1=\left(-\frac{\varepsilon_0V_0}{a}+P_0\right)\mathbf{u}_z

La densidad de corriente es nula en esta región, por ser un dieléctrico ideal.

2.1.2 En la región a < z < a + b

Tenemos un medio óhmico entre dos placas a distinto potencial. En esta región el campo eléctrico vale

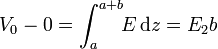
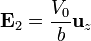
V_0-0=\int_a^{a+b}\!\! E\,\mathrm{d}z = E_2 b   \Rightarrow   \mathbf{E}_2 = \frac{V_0}{b}\mathbf{u}_z

Obsérvese que en esta región el campo va en sentido opuesto al de la otra zona. En ambos casos el campo va desde la placa de mayor central (la intermedia) a las de los extremos.

La densidad de corriente y el desplazamiento en esta región valen

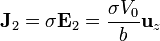
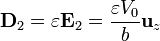
\mathbf{J}_2=\sigma\mathbf{E}_2 = \frac{\sigma V_0}{b}\mathbf{u}_z        \mathbf{D}_2=\varepsilon\mathbf{E}_2 = \frac{\varepsilon V_0}{b}\mathbf{u}_z

La corriente que circula entre la placa central y la superior es el flujo de la densidad volumétrica 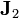\mathbf{J}_2 a través de una superficie paralela a las placas

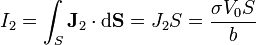
I_2 = \int_S \mathbf{J}_2\cdot\mathrm{d}\mathbf{S}=J_2 S=\frac{\sigma V_0 S}{b}

siendo S la superficie de las placas

2.2 Carga libre y voltaje de la placa central

2.2.1 Densidad volumétrica de carga libre

Al ser uniformes los campos en cada una de las regiones, la densidad volumétrica de carga libre es nula

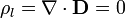
\rho_l = \nabla\cdot\mathbf{D} = 0

Sí hay densidades de carga libre sobre las placas conductoras. En todas ellas, por ser muy delgadas, podemos calcular la densidad superficial a partir del salto en \mathbf{D}, sin necesidad de distinguir entre una y otra cara de la placa.

2.2.2 Carga superficial en la placa de z = 0

Para la placa en z = 0, el vector desplazamiento en la parte superior es 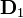\mathbf{D}_1, mientras que en la parte inferior es nulo, ya que en el exterior de un condensador ideal no hay campo eléctrico. Por tanto

\sigma_l(0) = \mathbf{n}\cdot[\mathbf{D}] = \mathbf{u}_z\cdot\left(\left(-\frac{\varepsilon_0 V_0}{a}+P_0\right)\mathbf{u}_z-\mathbf{0}\right) = -\frac{\varepsilon_0V_0}{a}+P_0

y la carga total en dicha placa

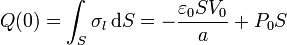
Q(0) = \int_S\sigma_l\,\mathrm{d}S = -\frac{\varepsilon_0SV_0}{a}+P_0S

2.2.3 Carga en la placa central

La densidad de carga libre en la place central vale

\sigma_l(a) = \mathbf{n}\cdot[\mathbf{D}] = \mathbf{u}_z\cdot\left(\frac{\varepsilon V_0}{b}\mathbf{u}_z - \left(-\frac{\varepsilon_0 V_0}{a}+P_0\right)\mathbf{u}_z\right) = \frac{\varepsilon a + \varepsilon_0 b}{ab}V_0- P_0

y la carga libre total de esta placa es

Q(a) = \int_S\sigma_l\mathrm{d}S = \frac{(\varepsilon a + \varepsilon_0 b)S}{ab}V_0- P_0S

2.2.4 Carga en la placa superior

Siguiendo el mismo método

\sigma_l(+b) = \mathbf{n}\cdot[\mathbf{D}] = \mathbf{u}_z\cdot\left(\mathbf{0}-\frac{\varepsilon V_0}{b}\mathbf{u}_z\right) = -\frac{\varepsilon V_0}{b}

y la carga libre total de esta placa es

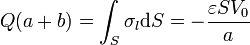
Q(a+b) = \int_S\sigma_l\mathrm{d}S = -\frac{\varepsilon SV_0}{a}

2.2.5 Condición para el potencial

Si queremos que la carga de la placa central sea nula el voltaje debe valer

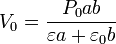
V_0 = \frac{P_0ab}{\varepsilon a + \varepsilon_0 b}

2.3 Estado estacionario tras la desconexión

Una vez que se desconecta el generador, el potencial de la placa central deja de estar fijado. El sistema evoluciona hasta alcanzar un nuevo estado estacionario.

Lo que caracteriza a este estado estacionario no es, de entrada, que la placa central esté descargada, o que su potencial sea nulo, sino que el sistema no depende del tiempo.

2.3.1 Campo en el medio óhmico

Si aplicamos la ley de conservación de la carga a la placa central tenemos que

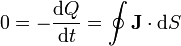
0 = -\frac{\mathrm{d}Q}{\mathrm{d}t}=\oint\mathbf{J}\cdot\mathrm{d}S

Esta integral se compone, en principio, de dos partes: una, que da la corriente a lo largo del cable conectado a la placa, pero ésta es nula por estar el generador desconectado; la otra corresponde a la corriente a través del medio óhmico. Por tanto

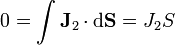
0 = \int \mathbf{J}_2\cdot\mathrm{d}\mathbf{S}= J_2S   \Rightarrow   \mathbf{J}_2=\mathbf{0}

y si no hay corriente, tampoco hay campo, por ser un medio óhmico

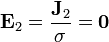
\mathbf{E}_2 = \frac{\mathbf{J}_2}{\sigma}=\mathbf{0}

Si el campo eléctrico en el medio óhmico es nulo, también lo será el vector desplazamiento en dicho medio.

2.3.2 Potencial de la placa central

El potencial de la placa central verifica

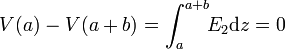
V(a) - V(a+b) = \int_a^{a+b}\!\! E_2\mathrm{d}z=0   \Rightarrow   V(a) = V(a+b)=0\,

esto es, la placa central se encuentra también a tierra.

2.3.3 Campo en el medio polarizado

El campo eléctrico en el medio polarizado es también nulo

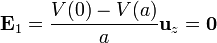
\mathbf{E}_1 = \frac{V(0)-V(a)}{a}\mathbf{u}_z = \mathbf{0}

no así el vector desplazamiento

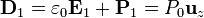
\mathbf{D}_1 =\varepsilon_0\mathbf{E}_1+\mathbf{P}_1 = P_0\mathbf{u}_z

2.3.4 Carga en la placa central

Al haber una discontinuidad en el vector desplazamiento, debe haber una densidad de carga en la placa central

\sigma_l(a) = \mathbf{n}\cdot[\mathbf{D}] = \mathbf{u}_z\cdot\left(\mathbf{0} -P_0\mathbf{u}_z\right) = -P_0

y la carga libre total de esta placa es

Q(a) = \int_S\sigma_l\mathrm{d}S = -P_0S\,

2.3.5 Carga en las placas exteriores

También existe una carga, opuesta a la anterior, en la placa situada en z = 0

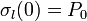
\sigma_l(0) = P_0\,        Q(0) = P_0S\,

En la placa superior, en cambio, la carga es nula, por ser nulo el campo a ambos lados

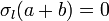\sigma_l(a+b)=0\,        Q(a + b) = 0

2.4 Estado transitorio

Para estudiar la evolución del sistema, supondremos que en cada instante la placa central posee un cierto valor V(t) que hemos de determinar. Su valor inicial será el calculado en el segundo apartado.

En cada instante, la carga de la placa central será, de acuerdo con el cálculo anterior

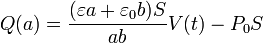
Q(a) = \frac{(\varepsilon a + \varepsilon_0 b)S}{ab}V(t)- P_0S

mientras que la corriente que fluye a través del medio óhmico es

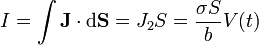
I=\int \mathbf{J}\cdot\mathrm{d}\mathbf{S}=J_2S = \frac{\sigma S}{b}V(t)

Aplicando ahora la ley de conservación de la carga a una superficie que envuelve a la placa central resulta

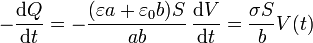
-\frac{\mathrm{d}Q}{\mathrm{d}t}= -\frac{(\varepsilon a + \varepsilon_0 b)S}{ab}\,\frac{\mathrm{d}V}{\mathrm{d}t} = \frac{\sigma S}{b}V(t)

lo que se puede escribir como

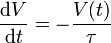
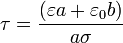
\frac{\mathrm{d}V}{\mathrm{d}t} = -\frac{V(t)}{\tau}         \tau = \frac{(\varepsilon a + \varepsilon_0 b)}{a\sigma}

La solución de esta ecuación diferencial es

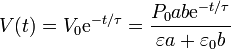
V(t) = V_0\mathrm{e}^{-t/\tau} =\frac{P_0ab\mathrm{e}^{-t/\tau}}{\varepsilon a + \varepsilon_0 b}

Este resultado indica que el voltaje decae exponencialmente desde su valor inicial hasta el potencial nulo final.

Aplicando las fórmulas obtenidos en el primer apartado, sustituyendo V0 por V(t) tenemos los campos en cada instante en cada región.

En particular, la carga de la placa central vareía con el tiempo, pasando de ser nula a tener un valor distinto de cero:

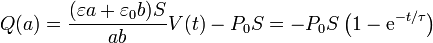
Q(a) = \frac{(\varepsilon a + \varepsilon_0 b)S}{ab}V(t)- P_0S = -P_0S\left(1-\mathrm{e}^{-t/\tau}\right)

Es una pregunta razonable el analizar por qué, si el sistema se está “descargando”, la placa central se está cargando. La razón es que las cargas de polarización asociadas a P0 atraen a cargas libres que se depositan en la placa.

Obtenido de "http://tesla.us.es/wiki/index.php/Descarga_de_un_condensador_con_un_medio_polarizado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace