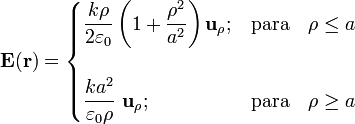Entrar Página Discusión Historial Go to the site toolbox

Cilindro relleno de una densidad de carga no uniforme

De Laplace

Contenido

1 Enunciado

El interior de un tubo cilínndrico de radio a y longitud indefinida está ocupado por un gas que presenta una distribución volumétrica de carga eléctrica, ρq, que varía con la distancia ρ al eje del tubo, según la ley

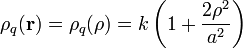
\rho_q(\mathbf{r})=\rho_q(\rho)=k\left(1+\frac{2\rho^2}{a^2}\right)

Inicialmente, no hay más cargas en el sistema.

  1. Determine la cantidad de carga contenida en una porción del tubo de longitud h, así como la expresión del campo eléctrico en todos los puntos del espacio.
  2. ¿Qué distribución superficial de carga debe añadirse en la superficie del tubo para que el campo eléctrico exterior sea nulo? Para ese caso, determine el potencial electrostático en todos los puntos del espacio.
  3. Supóngase que en el punto 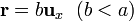\mathbf{r}= b\mathbf{u}_x\;\; (b < a) se encuentra una molécula de agua con momento dipolar 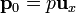\mathbf{p}_0 = p\mathbf{u}_x. ¿Cómo es la fuerza que el gas ejerce sobre ella? ¿A qué se reduce la fuerza si b = 0?

2 Carga y campo eléctrico

Puesto que la densidad volumétrica de carga sólo depende de la variable ρ (distancia al eje z), la cantidad de carga que hay dentro de una sección de tubo de longitud h se calcula integrado la densidad volumétrica en cualquier elemento de volumen que tenga dicha altura:


\left.\begin{array}{r}\Delta Q=\int_{\Delta \tau}\!\rho_q(\mathbf{r}')\mathrm{d}\tau'\\ \\ \mathrm{d}\tau'=\rho'\mathrm{d}\rho'\mathrm{d}\varphi'\mathrm{d}z'\end{array}\right\}\;\Longrightarrow\; \Delta Q=k\int_0^{2\pi}\!\mathrm{d}\varphi'\int_z^{z+h}\!\mathrm{d}z'\int_0^a\!\rho'\left[1+2\left(\frac{\rho'}{a}\right)^2\right]\mathrm{d}\rho'=2k\pi a^2

Para calcular el campo eléctrico creado por la distribución podemos utilizar diversos procedimientos. Por ejemplo, aplicar la ley de Gauss integral en un recinto con simetría cilíndrica, o bien, resolver la ecuación diferencial que para cada punto del espacio nos proporciona la versión local de dicha ley de Gauss. En cualquier caso, es esencial determinar las propiedades geométricas del campo eléctrico: como lo distribución de carga 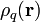\rho_q (\mathbf{r}) es estática, dicho campo va a ser irrotacional y, en consecuencia, derivará de un potencial electrostático 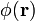\phi(\mathbf{r}). Como la distribución de carga que lo produce tiene una longitud indefinida y sólo depende de la distancia ρ al eje z, el valor de dicho campo escalar en un punto del espacio P(\rho,\varphi,z) no será función de las coordenadas cilíndricas \varphi y z. 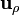En consecuencia, el campo eléctrico sólo tiene componente en la dirección de \mathbf{u}_\rho y ésta sólo depende de la variable ρ:

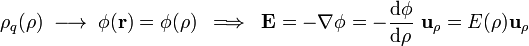
\rho_q (\rho)\;\longrightarrow\;\phi(\mathbf{r})=\phi(\rho)\;\;\Longrightarrow\;\;\mathbf{E}=-\nabla \phi=-\frac{\mathrm{d}\phi}{\mathrm{d}\rho}\ \mathbf{u}_\rho=E(\rho)\mathbf{u}_\rho


2.1 Versión integral de la ley de Gauss

Consideremos un volumen cilíndrico τ(ρ), coaxial con la distribución de carga, de radio y altura arbitrarias ρ y Δz, respectivamente. Según la ley de Gauss, el flujo del campo eléctrico a través de la superficie cerrada 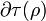\partial\tau (\rho) que limita dicho volumen es proporcional a la carga eléctrica encerrada:

La superficie cerrada 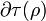\partial\tau (\rho) está formada por los discos Σ1 y Σ2, contenidos en sendos planos perpendiculares al eje z, y la superficie cilíndrica lateral ΣL. Sólo a través de esta última el flujo del campo eléctrico será no nulo:

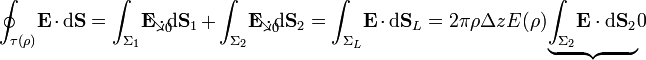
\oint_{\tau(\rho)}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=\int_{\Sigma_1}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}_1\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\mathop{\searrow}_{0}\;\;\;\;\,+\int_{\Sigma_2}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}_2\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\mathop{\searrow}_{0}\;\;\;\;\,=\int_{\Sigma_L}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}_L=2\pi\rho\Delta z E(\rho)\mathop{\underbrace{\int_{\Sigma_2}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}_2}}{0}


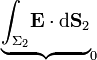
\mathop{\underbrace{\int_{\Sigma_2}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}_2}}_{0}

Por otra parte, la cantidad de carga encerrada dentro del volumen τ(ρ), va a depender tanto de su altura Δz, como del radio ρ:

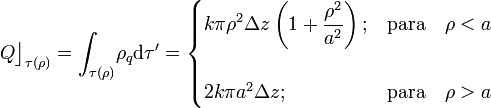
Q\big\rfloor_{\tau(\rho)}=\int_{\tau(\rho)}\!\rho_q \mathrm{d}\tau'=\begin{cases}\displaystyle k\pi \rho^2\Delta z\left(1+\frac{\rho^2}{a^2}\right); & \mathrm{para}\quad \rho<a \\ \\ 2k\pi a^2\Delta z; & \mathrm{para}\quad \rho>a \end{cases}

Y exigiendo que se verifique la ley de Gauss, se obtiene la expresión del campo elécgtrico para todos los puntos del espacio:

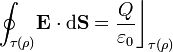
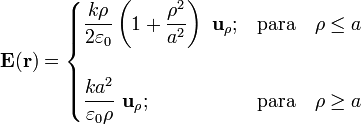
\oint_{\tau(\rho)}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q}{\varepsilon_0}\bigg\rfloor_{\tau(\rho)}   \Rightarrow   \mathbf{E}(\mathbf{r})=\begin{cases}\displaystyle \frac{k\rho}{2\varepsilon_0}\left(1+\frac{\rho^2}{a^2}\right)\ \mathbf{u}_\rho; & \mathrm{para}\quad \rho\le a \\ \\ \displaystyle\frac{k a^2}{\varepsilon_0\rho}\ \mathbf{u}_\rho; & \mathrm{para}\quad \rho\ge a \end{cases}

Obsérvese que al considerar que sólo la distribución volumétrica de carga es la fuente del campo eléctrico, éste va a presentar continuidad en la superficie cilíndrica ρ = a.

2.2 Versión local de la ley de Gauss

La versión local de la ley de Gauss, junto con las propiedades de simetría del campo eléctrico antes determinadas, nos lleva al siguiente conjunto de ecuaciones diferenciales:

\left.\begin{array}{r}\displaystyle\nabla\cdot\mathbf{E}=\frac{\rho_q}{\varepsilon_0}\\ \\ \mathbf{E}(\mathbf{r})=E(\rho)\mathbf{u}_\rho\end{array}\right\} \quad\longrightarrow\quad\frac{1}{\rho}\frac{\mathrm{d}}{\mathrm{d}\rho}\big[\rho E(\rho)\big]=\begin{cases}\displaystyle \frac{k}{\varepsilon_0}\left(1+\frac{2\rho^2}{a^2}\right); & \mathrm{para}\quad \rho<a \\ \\ 0; & \mathrm{para}\quad \rho>a \end{cases}

Las soluciones generales a estas ecuaciones son:

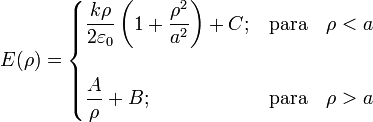
E(\rho)=\begin{cases}\displaystyle \frac{k \rho}{2\varepsilon_0}\left(1+\frac{\rho^2}{a^2}\right)+C; & \mathrm{para}\quad \rho<a \\ \\ \displaystyle \frac{A}{\rho}+B; & \mathrm{para}\quad \rho>a \end{cases}

donde A, B y C son constantes a determinar por las condiciones de contorno. Como el campo eléctrico debe anularse en puntos muy alejados de la distribución (cuando 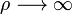\rho\longrightarrow\infty), se tendrá que B = 0. Por otra parte, la carga eléctrica contenida en un cilindro de radio \rho\longrightarrow 0 tiende a ser cero; por tanto, el campo eléctrico también debe anularse cuando \rho\longrightarrow 0 y, en consecuencia, C = 0. Finalmente, el valor de A se determina exigiendo la continuidad de la componente normal del campo en ρ = a, ya que en este apartado no se considera la existencia de una distribución superficial de carga eléctrica en dicha superficie, de forma que E(a + ) = E(a − ). Se obtiene, por tanto,

\mathbf{E}(\mathbf{r})=\begin{cases}\displaystyle \frac{k\rho}{2\varepsilon_0}\left(1+\frac{\rho^2}{a^2}\right) \mathbf{u}_\rho; & \mathrm{para}\quad \rho\le a \\ \\ \displaystyle\frac{k a^2}{\varepsilon_0\rho}\ \mathbf{u}_\rho; & \mathrm{para}\quad \rho\ge a \end{cases}

3 Distribución superficial para anular el campo

3.1 Potencial electrostático en la nueva situación

4 Fuerza sobre una molécula de agua

Obtenido de "http://tesla.us.es/wiki/index.php/Cilindro_relleno_de_una_densidad_de_carga_no_uniforme"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace