Descarga de un condensador con un medio polarizado
De Laplace
Revisión a fecha de 15:32 19 jun 2008; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
El sistema de la figura está formado por tres placas conductoras ideales, planas y paralelas, todas de área S. Todas las placas pueden suponerse muy delgadas. Entre la placa “1” y la “2” hay un dieléctrico ideal de espesor a, caracterizado porque presenta una polarización uniforme y constante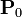 , perpendicular a dichas placas. Entre las placas “2” y “3”, separadas una distancia b, hay un medio óhmico de conductividad σ y permitividad
, perpendicular a dichas placas. Entre las placas “2” y “3”, separadas una distancia b, hay un medio óhmico de conductividad σ y permitividad  . Las dos regiones entre las placas están inicialmente descargadas. La placa central se encuentra conectada a un generador, que fija una diferencia de potencial V0 respecto a las otras dos placas, ambas a tierra.
. Las dos regiones entre las placas están inicialmente descargadas. La placa central se encuentra conectada a un generador, que fija una diferencia de potencial V0 respecto a las otras dos placas, ambas a tierra.
- Determine los campos y corrientes en el sistema cuando éste se halla en régimen estacionario.
- Calcule las distribuciones estacionarias de carga libre en el sistema. Ajuste el valor de V0 para que la placa central esté descargada. Este valor se usará en los dos apartados siguientes.
- En un instante t = 0 se desconecta el generador. Halle la distribución de campos, corrientes y cargas libres en el sistema cuando se alcanza de nuevo una situación estacionaria.
- Calcule la evolución en el tiempo de los campos, las corrientes y la carga libre en las placas.
Desprecie los efectos de borde.
2 Solución
2.1 Estado estacionario antes de la desconexión
La clave para resolver este apartado es observar que la placa central es un conductor a potencial fijado y por tanto separa completamente los problemas a un lado y al otro de ella. Así, en lugar de un problema complicado tenemos dos problemas sencillos:
- En 0 < z < a tenemos una región polarizada uniformemente con polarización
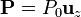
- situada entre dos conductores a potenciales 0 y V0, respectivamente.
- Si suponemos despreciables los efectos de borde, dado que el medio entre las placas es homogéneo, el campo eléctrico es uniforme entre las placas y va en la dirección perpendicular a ellas:
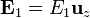
- El valor del campo lo obtenemos de la diferencia de potencial entre las placas:
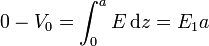

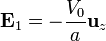
- y, conocidos el campo y la polarización tenemos el vector desplazamiento: