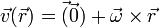Campos equiproyectivos y campo de momentos

De Laplace

Revisión a fecha de 09:41 18 jun 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado del teorema
2 Demostración
- 2.1 Campo equiproyectivo implica campo de momentos
- 2.2 Campo de momentos implica campo equiproyectivo

1 Enunciado del teorema

Un campo vectorial es equiproyectivo sí y solo sí es un campo de momentos de un vector deslizante.

2 Demostración

2.1 Campo equiproyectivo implica campo de momentos

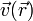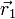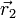La condición de equiproyectividad para un campo vectorial $\vec{v}(\vec{r})$ puede expresarse como que para cualesquiera dos puntos $\vec{r}_1$ y $\vec{r}_2$ se verifica

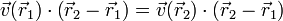
$\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)$

se trata de demostrar que si se cumple esta condición, 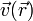$\vec{v}(\vec{r})$ puede escribirse en la forma

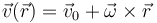
$\vec{v}(\vec{r})=\vec{v}_0+\vec{\omega}\times\vec{r}$

Para demostrarlo, suponemos un sistema de referencia con origen en el punto $\vec{0}$ y cuyos ejes vienen caracterizados por los vectores unitarios $\vec{\imath}$ , $\vec{\jmath}$ y $\vec{k}$ .

2.1.1 Referencia al origen

Definamos en primer lugar el campo, también equiproyectivo

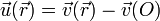
$\vec{u}(\vec{r}) = \vec{v}(\vec{r})-\vec{v}(O)$

Este campo cumple

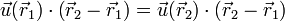
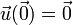
$\vec{u}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{u}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)$ $\vec{u}(\vec{0})=\vec{0}$

2.1.2 Equiproyectividad aplicada a cada vector de la base con el origen

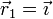Si aplicamos la condición de equiproyectividad de $\vec{u}$ a los dos puntos $\vec{r}_1=\vec{\imath}$ y $\vec{0}$ nos queda

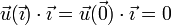
$\vec{u}(\vec{\imath})\cdot\vec{\imath} = \vec{u}(\vec{0})\cdot\vec{\imath} = 0$

esto quiere decir que 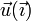$\vec{u}(\vec{\imath})$ es ortogonal a $\vec{\imath}$ , esto es, no posee componente $X$ y puede escribirse como

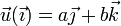
$\vec{u}(\vec{\imath}) = a\vec{\jmath} + b\vec{k}$

Aplicando el mismo razonamiento a $\vec{\jmath}$ y a $\vec{k}$ nos queda

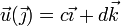
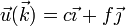
$\vec{u}(\vec{\jmath}) = c\vec{\imath} + d\vec{k}$ $\vec{u}(\vec{k}) = c\vec{\imath} + f\vec{\jmath}$

2.1.3 Equiproyectividad aplicada a pares de vectores de la base

La condición de equiproyectividad también puede aplicarse al par de puntos $\vec{\imath}$ y $\vec{\jmath}$ . En este caso tenemos

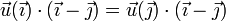
$\vec{u}(\vec{\imath})\cdot\left(\vec{\imath}-\vec{\jmath}\right) = \vec{u}(\vec{\jmath})\cdot\left(\vec{\imath}-\vec{\jmath}\right)$ $\Rightarrow$ $-a = c\,$

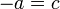
Operando igualmente con los otros dos pares nos queda

$-b = e\,$ $-d = f\,$

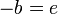
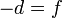
Si llamamos

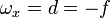
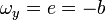
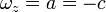
$\omega_x = d = -f\,$ $\omega_y = e = -b\,$ $\omega_z = a = -c\,$

el valor de $\vec{u}$ en $\vec{\imath}$ , $\vec{\jmath}$ y $\vec{k}$ se escribe

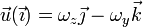
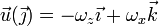
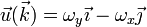
$\vec{u}(\vec{\imath}) = \omega_z\vec{\jmath}-\omega_y\vec{k}$ $\vec{u}(\vec{\jmath}) = -\omega_z\vec{\imath}+\omega_x\vec{k}$ $\vec{u}(\vec{k}) = \omega_y\vec{\imath}-\omega_x\vec{\jmath}$

2.1.4 Aplicación a un punto genérico

Si ahora aplicamos la condición de equiproyectividad a un punto cualquiera

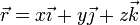
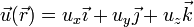
$\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$ $\vec{u}(\vec{r})=u_x\vec{\imath}+u_y\vec{\jmath}+u_z\vec{k}$

y al origen nos queda

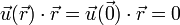
$\vec{u}(\vec{r})\cdot\vec{r}=\vec{u}(\vec{0})\cdot\vec{r}= 0$

esto es, que el campo en cada punto es ortogonal al vector de posición de dicho punto.

Si ahora aplicamos la condición al mismo punto $\vec{r}$ y al punto $\vec{\imath}$ tenemos

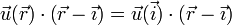
$\vec{u}(\vec{r})\cdot\left(\vec{r}-\vec{\imath}\right)=\vec{u}(\vec{i})\cdot\left(\vec{r}-\vec{\imath}\right)$ $\Rightarrow$

- u x = ω z y - ω y z

y aplicándolo al mismo punto con los otros vectores de la base

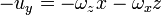
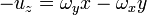
$-u_y=-\omega_zx-\omega_xz\,$ $-u_z=\omega_yx-\omega_xy\,$

esto es

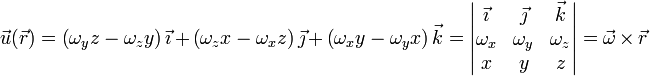
$\vec{u}(\vec{r}) = \left(\omega_yz-\omega_zy\right)\vec{\imath}+\left(\omega_zx-\omega_xz\right)\vec{\jmath}+\left(\omega_xy-\omega_yx\right)\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ x & y & z\end{matrix}\right|=\vec{\omega}\times\vec{r}$

y volviendo a nuestro campo original, $\vec{v}$

$\vec{v}(\vec{r})=\vec(\vec{0}) +\vec{\omega}\times\vec{r}$

Campos equiproyectivos y campo de momentos

De Laplace

Contenido

1 Enunciado del teorema

2 Demostración

2.1 Campo equiproyectivo implica campo de momentos

2.1.1 Referencia al origen

2.1.2 Equiproyectividad aplicada a cada vector de la base con el origen

2.1.3 Equiproyectividad aplicada a pares de vectores de la base

2.1.4 Aplicación a un punto genérico

2.2 Campo de momentos implica campo equiproyectivo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES