Ejemplo paramétrico de movimiento plano

De Laplace

Revisión a fecha de 18:26 16 dic 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Velocidad y aceleración
- 2.1 Velocidad
  - 2.1.1 Empleando el sistema de referencia “1”
  - 2.1.2 Empleando el sistema de referencia “2”
3 CIR en el sistema “1”
4 CIR en el sistema “2”

1 Enunciado

La escuadra $O 2 X 2 Y 2$ (sólido “2”) se mueve respecto a la escuadra $O 1 X 1 Y 1$ (sólido “1”) de forma que su origen de coordenadas, $O 2$ , verifica la ecuación paramétrica

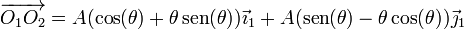
$\overrightarrow{O_1O_2} =A(\cos(\theta)+\theta \,\mathrm{sen}(\theta))\vec{\imath}_1 + A(\mathrm{sen}(\theta)-\theta \cos(\theta))\vec{\jmath}_1$

siendo $θ = θ(t)$ el ángulo que el eje $O 2 X 2$ forma con el $O 1 X 1$ .

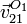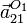Calcule la velocidad y la aceleración instantáneas del punto $O 1$ en el movimiento {21}: $\vec{v}^{O_1}_{21}$ y $\vec{a}^{O_1}_{21}$ .
Determine la posición del CIR $I 21$ y exprésela empleando el sistema de referencia ligado al sólido “1”.
Exprese la posición del mismo punto $I 21$ en el sistema de referencia ligado al sólido “2”.

2 Velocidad y aceleración

2.1 Velocidad

La velocidad del punto $O 1$ , como parte del sólido “2” respecto al “1”, 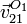$\vec{v}^{O_1}_{21}$ , puede calcularse de diferentes formas.

2.1.1 Empleando el sistema de referencia “1”

Debemos hallar la velocidad cuya posición no conocemos en todo instante. El punto cuya posición sí conocemos y podemos derivar es $O 2$ . Por ello, debemos usar la expresión del campo de velocidades

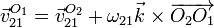
$\vec{v}^{O_1}_{21}=\vec{v}^{O_2}_{21} + \omega_{21}\vec{k}\times\overrightarrow{O_2O_1}$

Veamos cada término por separado.

La velocidad de $O 2$ en el movimiento {21} sí puede hallarse derivando respecto al tiempo, por aplicación de la regla de la cadena.

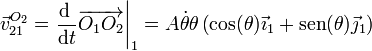
$\vec{v}^{O_2}_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{O_1O_2}\right|_1=A\dot{\theta}\theta\left(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\right)$

La velocidad angular es inmediata, puesto que conocemos el ángulo que forman los ejes $O X 1$ y $O X 2$

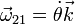
$\vec{\omega}_{21}=\dot{\theta}\vec{k}$

El vector de posición relativo es el opuesto al que aparece en el enunciado

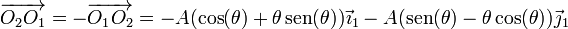
$\overrightarrow{O_2O_1}=-\overrightarrow{O_1O_2} =-A(\cos(\theta)+\theta \,\mathrm{sen}(\theta))\vec{\imath}_1 - A(\mathrm{sen}(\theta)-\theta \cos(\theta))\vec{\jmath}_1$

Reuniendo todo esto obtenemos la velocidad del punto $O 1$

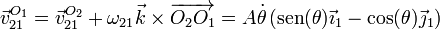
$\vec{v}^{O_1}_{21}=\vec{v}^{O_2}_{21} + \omega_{21}\vec{k}\times\overrightarrow{O_2O_1}=A\dot{\theta}\left(\mathrm{sen}(\theta)\vec{\imath}_1-\cos(\theta)\vec{\jmath}_1\right)$

2.1.2 Empleando el sistema de referencia “2”

Puesto que el punto $O 1$ es el origen de coordenadas del sistema de referencia “1”, puede parecer más intuitivo considerar el movimiento inverso, del sólido “1” respecto al “2”. Las velocidades de los movimientos inversos se relacionan por la igualdad

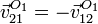
$\vec{v}^{O_1}_{21}=-\vec{v}^{O_1}_{12}$

Para hallar el segundo miembro, expresaremos la posición del punto $O 1$ en el sistema de referencia ligado al sólido “2”. El vector de posición relativo es, según dijimos,

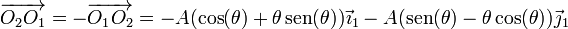
$\overrightarrow{O_2O_1}=-\overrightarrow{O_1O_2} =-A(\cos(\theta)+\theta \,\mathrm{sen}(\theta))\vec{\imath}_1 - A(\mathrm{sen}(\theta)-\theta \cos(\theta))\vec{\jmath}_1$

Esta vector aun está expresado en el sistema de referencia “1”. Para pasar al “2” debemos relacionar las bases respectivas. Las relaciones son

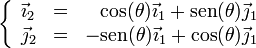
$\left\{\begin{array}{lcr} \vec{\imath}_2 & = & \cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1 \\ \vec{\jmath}_2 & = & -\mathrm{sen}(\theta)\vec{\imath}_1 + \cos(\theta)\vec{\jmath}_1 \end{array}\right.$

Podemos obtener el vector de expresión en la base “2” simplemente observando que

$\overrightarrow{O_2O_1}=-A(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta))\vec{\jmath}_1-A\theta(\mathrm{sen}(\theta)\vec{\imath}_1 - \cos(\theta))\vec{\jmath}_1$

donde podemos reconocer los vectores de la base, por lo que

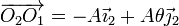
$\overrightarrow{O_2O_1}=-A\vec{\imath}_2+A\theta\vec{\jmath}_2$

La obtención de la velocidad inversa es entonces trivial

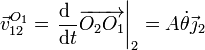
$\vec{v}^{O_1}_{12}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{O_2O_1}\right|_2 = A\dot{\theta}\vec{\jmath}_2$

y la velocidad que pide el enunciado es

$\vec{v}^{O_1}_{21}=-\vec{v}^{O_1}_{21}=- A\dot{\theta}\vec{\jmath}_2$

3 CIR en el sistema “1”

4 CIR en el sistema “2”

Ejemplo paramétrico de movimiento plano

De Laplace

Contenido

1 Enunciado

2 Velocidad y aceleración

2.1 Velocidad

2.1.1 Empleando el sistema de referencia “1”

2.1.2 Empleando el sistema de referencia “2”

3 CIR en el sistema “1”

4 CIR en el sistema “2”

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES