Ejemplo paramétrico de movimiento plano

De Laplace

Contenido 1 Enunciado 2 Velocidad y aceleración 2.1 Velocidad 2.2 =Empleando el sistema de referencia “1” 3 CIR en el sistema “1” 4 CIR en el sistema “2”

1 Enunciado

La escuadra O₂X₂Y₂ (sólido “2”) se mueve respecto a la escuadra O₁X₁Y₁ (sólido “1”) de forma que su origen de coordenadas, O₂, verifica la ecuación paramétrica

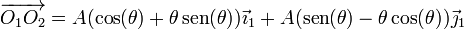
siendo θ = θ(t) el ángulo que el eje O₂X₂ forma con el O₁X₁.

1. Calcule la velocidad y la aceleración instantáneas del punto O₁ en el movimiento {21}: 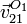y .
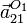2. Determine la posición del CIR I₂₁ y exprésela empleando el sistema de referencia ligado al sólido “1”.
3. Exprese la posición del mismo punto I₂₁ en el sistema de referencia ligado al sólido “2”.

2 Velocidad y aceleración

2.1 Velocidad

La velocidad del punto O₁, como parte del sólido “2” respecto al “1”,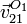 puede calcularse de diferentes formas.

2.2 =Empleando el sistema de referencia “1”

Debemos hallar la velocidad cuya posición no conocemos en todo instante. El punto cuya posición sí conocemos y podemos derivar es O₂. Por ello, debemos usar la expresión del campo de velocidades

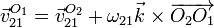
Veamos cada término por separado.

La velocidad de O₂ en el movimiento {21} sí puede hallarse derivando respecto al tiempo, por aplicación de la regla de la cadena.

3 CIR en el sistema “1”

4 CIR en el sistema “2”