Dos discos rodando en aro
De Laplace
Contenido[ocultar] |
1 Enunciado
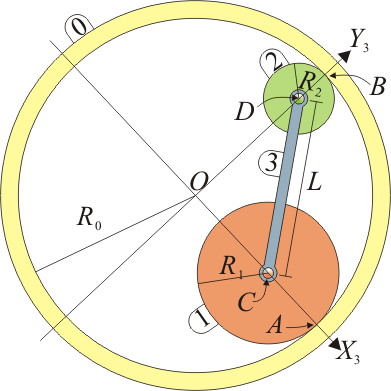
Se tiene el sistema de la figura, formado por dos discos “1” y “2” de radios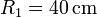 
y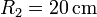 
cuyos centros, C y D, están unidos por una barra rígida “3” de longitud 
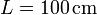. Las dos ruedas del artilugio ruedan sin deslizar por la superficie interior de un aro “0” de radio 
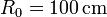, siendo A y B los respectivos puntos de contacto. El centro del disco “1” gira con velocidad angular constante 
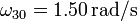en sentido antihorario respecto al aro exterior “0”.
- Determine las cinco velocidades angulares relativas restantes.
- Localice los seis centros instantáneos de rotación.
Sugerencia: Emplee el sistema de ejes ligado al sólido “3” de la figura, tal que el eje OX3 pasa por el centro del disco “1”.
2 Velocidad angulares
2.1 Movimiento {30}
El enunciado nos da la velocidad angular con la que gira el punto C, centro del disco 1 alrededor del centro del aro “0”. Este punto pertenece tanto al sólido “1” como al “3” por tratarse de la articulación de la barra con el disco. Esta velocidad angular es la que posee toda la barra “3” en su rotación alrededor de O. Por eso, los subíndices del dato se refieren al movimiento {30} (y no al {10} ya que como veremos, el disco 1 posee una velocidad angular diferente):
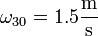
2.2 Movimiento {10}
Para hallar la velocidad angular observamos que este movimiento es una rotación alrededor del punto de contacto, A, y por tanto la velocidad del centro del disco “1” en este movimiento es
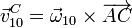
Por otro lado tenemos que la velocidad de C, considerado como parte de “3”, es una rotación alrededor de O
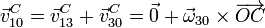
Igualando ambas velocidades llegamos a la relación
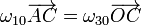
Los vectores de posición relativos valen, en el sistema de referencia indicado:
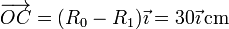
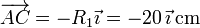
De aquí obtenemos la velocidad angular
3 Movimiento {31}
La velocidad angular del movimiento {31} es inmediata por aplicación de la ley de composición correspondiente
