Entrar Página Discusión Historial Go to the site toolbox

Corteza esférica conductora con distribución concéntrica

De Laplace

Contenido

1 Enunciado

Una corteza conductora esférica cuyos radios interior y exterior valen 3a y 6a respectivamente, es concéntrica con una esfera de radio 2a cargada uniformemente en volumen con una densidad de carga ρ0.
  1. Para el caso de que la corteza esté aislada y descargada, obtenga la expresión del campo eléctrico en todo el espacio, así como las densidades de carga en la corteza conductora.
  2. Si el conductor se conecta a tierra, ¿cuál es la nueva expresión del campo en todo el espacio? ¿Cuál es ahora la distribución de carga en el conductor?
  3. ¿Qué cambio experimenta la energía electrostática del sistema al pasar de la situación del apartado (a) a la del apartado (b)?

2 Solución

2.1 Corteza conductora aislada y descargada

Si la corteza conductora se encuentra en equilibrio eléctrostático, no puede presentar densidades volumétricas de carga eléctrica. Sólo puede haber distribuciones netas de carga en las superficies que la delimitan; es decir, en

\Sigma_\mathrm{C}^\mathrm{int}: r=3a\mathrm{;}\qquad \qquad\Sigma_\mathrm{C}^\mathrm{ext}: r=6a;

donde éstas están descritas en coordenadas esféricas, tomando el centro de simetría del sistema (punto O) como origen del sistema de referencia.

2.1.1 Distribuciones de carga eléctrica en el sistema

En consecuencia, la única distribución volumétrica presente en el sistema es la densidad uniforme ρ0 que hay en r < 2a:
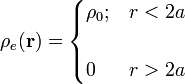
\rho_e(\mathbf{r})=\begin{cases} \rho_0\mathrm{;}& r<2a\\ \\ 0&r>2a \end{cases}

La cantidad total de carga de esta distribución es:

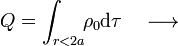
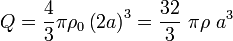
Q=\int_{r<2a}\!\! \rho_0 \mathrm{d}\tau\quad\longrightarrow \quad Q=\frac{4}{3}\pi\rho_0\left(2a\right)^3=\frac{32}{3}\ \pi\rho\ a^3

Esta carga en el hueco r < 3a, induce una cantidad de carga opuesta − Q en la cara interior de la corteza conductora para que se verifique la condición necesaria de campo eléctrico nulo en el conductor. Como la carga Q está distribuida uniformemente y produce un campo eléctrico radial, la carga en la superficie 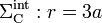\Sigma_\mathrm{C}^\mathrm{int}: r=3a se distribuirá también uniformemente. Por otra parte, como el conductor está aislado y descargado, su cantidad total de carga debe ser nula. 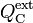Si llamamos Q_\mathrm{C}^\mathrm{int} y Q_\mathrm{C}^\mathrm{ext} a las cantidades de carga distribuidas en las caras interior y exterior de la corteza conductora, se tendrá:

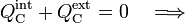
Q_\mathrm{C}^\mathrm{int}+Q_\mathrm{C}^\mathrm{ext}=0\quad \Longrightarrow\quad Q_\mathrm{C}^\mathrm{ext}=-Q_\mathrm{C}^\mathrm{int}=Q

También la carga Q se distribuirá uniformemente en la superficie exterior de la corteza \Sigma_\mathrm{C}^\mathrm{ext}, ya que ésta tiene simetría esférica y no hay otras cargas exteriores que pudiesen alterar dicha distribución. Por tanto, se tendrá que la distribución de cargas superficiales en el sistema es:

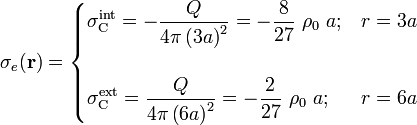
\sigma_e(\mathbf{r})=\begin{cases}\displaystyle \sigma_\mathrm{C}^\mathrm{int}=-\frac{Q}{4\pi\left(3a\right)^2}=-\frac{8}{27}\ \rho_0\ a\mathrm{;}& r=3a\\ \\ \displaystyle\sigma_\mathrm{C}^\mathrm{ext}=\frac{Q}{4\pi\left(6a\right)^2}=-\frac{2}{27}\ \rho_0\ a\mathrm{;}&r=6a \end{cases}

2.1.2 Campo eléctrico en el sistema

Para determinar la distribución del campo eléctrico aplicaremos la ley de Gauss:

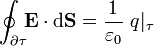
\oint_{\partial\tau}\!\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{1}{\varepsilon_0}\ q|_\tau

donde q | τ es la cantidad total de carga que hay dentro de la superficie \partial\tau. Como las distribuciones de carga estática determinadas anteriormente presentan todas simetría esférica, el campo eléctrico que producen es radial. Evaluando la ley de Gauss en una superficie esférica \partial\tau de radio r arbitrario y centrada en el punto O, se tendrá:

\mathbf{E}(\mathbf{r})=E(r)\mathbf{u}_r    \Rightarrow    \oint_{\partial\tau:\ r\,\mathrm{cte.}\,}\!\!\!\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=4\pi r^2 E(r)

La cantidad de carga dentro de \partial\tau depende del radio de ésta:

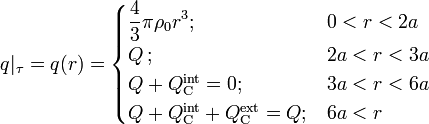
q|_\tau=q(r)=\begin{cases}\displaystyle \frac{4}{3}\pi\rho_0r^3\mathrm{;}& 0<r<2a\\ Q\,\mathrm{;}& 2a<r<3a\\ Q+Q_\mathrm{C}^\mathrm{int}=0\mathrm{;}& 3a<r<6a\\ Q+Q_\mathrm{C}^\mathrm{int}+Q_\mathrm{C}^\mathrm{ext}=Q\mathrm{;}& 6a<r\end{cases}      \Rightarrow     

Y aplicando ahora la ley de Gauss se obtiene la expresión del campo eléctrico en todo el espacio:

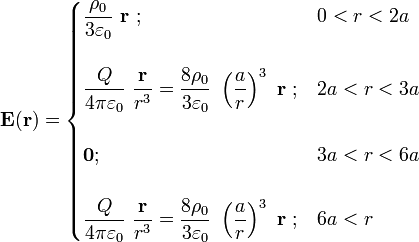
\mathbf{E} (\mathbf{r})=\begin{cases}\displaystyle \frac{\rho_0}{3\varepsilon_0}\ \mathbf{r}\ \mathrm{;}& 0<r<2a\\ \\ \displaystyle \frac{Q}{4\pi\varepsilon_0}\ \frac{\mathbf{r}}{r^3}=\frac{8\rho_0}{3\varepsilon_0}\ \left(\frac{a}{r}\right)^3\ \mathbf{r}\ \mathrm{;}& 2a<r<3a\\ \\ \mathbf{0}\mathrm{;}& 3a<r<6a\\ \\ \displaystyle \frac{Q}{4\pi\varepsilon_0}\ \frac{\mathbf{r}}{r^3}=\frac{8\rho_0}{3\varepsilon_0}\ \left(\frac{a}{r}\right)^3\ \mathbf{r}\ \mathrm{;}& 6a<r\end{cases}

2.2 Corteza conductora conectada a tierra

En esta situación, toda la corteza conductora estará a potencial nulo. En particular, las superficies

2.2.1 Distribuciones de carga eléctrica en el sistema

Obtenido de "http://tesla.us.es/wiki/index.php/Corteza_esf%C3%A9rica_conductora_con_distribuci%C3%B3n_conc%C3%A9ntrica"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace