Movimiento plano (G.I.T.I.)
De Laplace
Contenido |
1 Definición de movimiento plano
De entre los posibles movimientos de un sólido rígido, se dice que un sólido “2” realiza un movimiento plano respecto a un sólido “1” si los desplazamientos de todos sus puntos son permanentemente paralelos a un plano fijo en el sistema de referencia ligado al sólido 1. Este plano se denomina plano director, ΠD del movimiento plano. Cualquier plano paralelo a un plano director del movimiento {21} es también un plano director de dicho movimiento.
Así, por ejemplo, el movimiento que realiza el chasis de un coche, respecto a la calzada por la que éste circula, es un movimiento plano.
También lo es el movimiento de una de sus ruedas cuando el coche avanza en línea recta. Sin embargo, en ese caso, el plano director no es el plano de la calzada, sino uno perpendicular a ella.
Matemáticamente tenemos que, para todo punto del sólido debe cumplirse en todo instante que
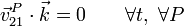
Siendo 
un vector constante, unitario y normal al plano director. Siempre podemos tomar el sistema de referencia ligado al sólido 1 de tal forma que el vector normal vaya en la dirección del eje OZ (o cualquier otra dirección fija que nos convenga)
Un movimiento plano de un sólido satisface, entre otras, las siguientes propiedades:
- Las velocidades de todos los puntos del sólidos se encuentran contenidas en planos paralelos
- Es la condición definitoria del movimiento plano.
- Las aceleraciones de todos los puntos se siempre paralelas al plano director
- Puesto que la identidad anterior se cumple en cada instante, podemos derivar en ella respecto al tiempo
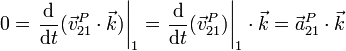
- La trayectoria de cada uno de los puntos es plana
- Puesto que la velocidad y la aceleración de cada punto son tangentes al plano director, el vector binormal de cada trayectoria es siempre perpendicular al plano y por tanto constante.
- La velocidad angular del movimiento {21} es perpendicular al plano director (o nula)
- Por tratarse de un movimiento rígido, para cualesquiera dos puntos del sólido 2 se cumple
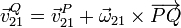
- Multiplicando aquí escalarmente por el vector normal al plano director
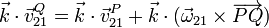
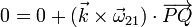
- Puesto que esta identidad debe cumplirse para cualquier par de puntos, la única posibilidad es que
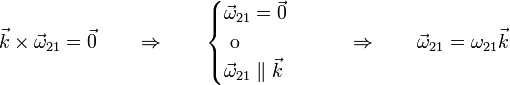
- La aceleración angular del movimiento {21} es perpendicular al plano director
- Es consecuencia inmediata de que la velocidad angular posea dirección constante
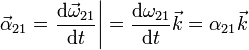
- El movimiento instantáneo {21} es de reposo, traslación o rotación, pero no helicoidal
- Si
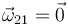entonces el movimiento {21} es un estado de reposo o es una traslación.
- Si la velocidad angular no es nula, la velocidad de deslizamiento vale 0
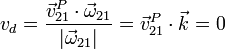
- y por tanto en ese caso el movimiento es una rotación.
- Un movimiento plano tiene tres grados de libertad
- Un movimiento rígido general tiene 6 grados de libertad, especificados por las tres componentes de la velocidad angular y las tres componentes de la velocidad de un punto. En un movimiento plano, la velocidad angular tiene una sola componente que puede variar, la normal al plano, y la velocidad de un punto tiene dos, tangentes al mismo plano
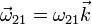
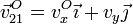
- Las especificación de esos 3 valores determina completamente el movimiento del sólido, que por tanto tiene 3 grados de libertad. En términos de variables, un movimiento plano queda descrito por la evolución temporal de dos coordenadas de un punto y del ángulo que forman los ejes de los triedros “2” y “1”.
- Las distribuciones de velocidades en planos paralelos al plano director son idénticas entre sí
- Si el movimiento es una traslación, evidentemente las distribuciones son idénticas, ya que todos los puntos tienen la misma velocidad.
- Si se trata de una rotación, el eje instantáneo de rotación es perpendicular al plano director, y por tanto, las distribuciones de las velocidades en planos perpendiculares a este eje (y paralelos al plano director) son idénticas.
- Esto quiere decir que para estudiar el movimiento plano basta con considerar lo que ocurre en uno de sus planos paralelos al plano director. Esto no implica que el sólido sea cilíndrico (esto es, que el sólido real no tiene por qué tener la misma forma en todos los planos paralelos al director).
