Problemas de Cinemática del sólido rígido (G.I.A.)

De Laplace

1 Determinación del vector rotación a partir de la velocidad en tres puntos

Dada las velocidades 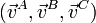en tres puntos no alineados de un sólido rígido (A,B,C), determina el vector que describe larotación instantánea del sólido rígido. ¿Que ocurre si los tres puntos están alineados?

2 Ejemplo de campo de velocidades de un sólido

Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,

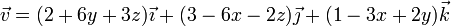
1. Prueba que corresponde al movimiento de un sólido rígido.
2. Determina la velocidad angular y la velocidad de deslizamiento.
3. Halla la ecuación del eje instantáneo de rotación y mínimo deslizamiento.

3 Campo de velocidades a partir de la velocidad en tres puntos

En un determinado instante, las posiciones de tres puntos de un sólido rígido, respecto de un sistema de referencia cartesiano OXYZ, vienen dadas por las ternas de coordenadas A(0,0,0), B(0,9,0), 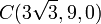. En el mismo instante, las velocidades instantáneas de estos tres puntos respecto a dicho sistema OXYZ son, respectivamente:

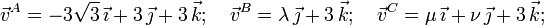
donde las componentes de los vectores posición y velocidad se miden en unidades base del SI. Calcula para dicho instante de tiempo:

1. Valores de λ, μ y ν.
2. Vector rotación total del sólido.
3. Velocidad de mínimo deslizamiento.
4. Eje instantáneo de rotación y mínimo deslizamiento.
5. Ligar geométrico de los puntos cuya velocidad es paralela a la recta

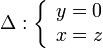
4 Ejemplos de reducciones cinemáticas

Encuentra las reducciones cinemáticas instantáneas pedidas de cada uno de estos movimientos

1. Una rueda de radio R que gira con velocidad angular constante ω alrededor de un eje perpendicular a ella que pasa por su centro. Encuentra la reducción canónica.
2. Una rueda de radio R rueda sin deslizar sobre una superficie horizontal de modo que su centro avanza con velocidad uniforme v₀. Encuentra la reducción en el centro y la reducción canónica.
3. Una rueda de radio R rueda y desliza con velocidad angular ω alrededor de un eje perpendicular a ella, de modo que el punto de contacto con el suelo tiene una vez relativa a éste de módulo v_des. Encuentra la reducción en el punto de contacto y la reducción canónica.
4. Un tornillo gira con velocidad angular uniforme ω y avanza con velocidad uniforme v paralelamente a su eje. Encuentra la reducción en el punto más alto de la superficie frontal del tornillo y la reducción canónica.

5 Triángulo en movimiento helicoidal

El triángulo de vértices A, B, y C constituye un sólido rígido en movimiento respecto al sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos:

1. Los vértices A y B permanecen en todo instante sobre el eje OZ, desplazándose ambos con igual velocidad instantánea .
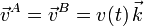2. El vértice C se mueve describiendo la hélice Γ, que en el sistema OXYZ está descrita por las ecuaciones paramétricas:

donde R y h son constantes conocidas. Se pide:

1. Indicar de forma razonada cual es el eje instantáneo de rotación y mínimo deslizamiento en este movimiento. Determinar el vector rotación total en términos de los datos expresados en el enunciado.
2. Expresar la componente normal de la aceleración del vértice C en un instante cualquiera, en función de los datos del enunciado.
3. Para el caso en que v(t) = v₀ (cte), y h = R / 2, calcular la aceleración del vértice C. Determinar la ley horaria s = s(t) con que el punto C describe su trayectoria.

6 Ejemplo de movimiento de precesión

El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular

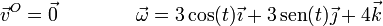
Consideremos el punto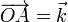

1. Determine la velocidad de este punto en cada instante.
2. Determine la aceleración de A en todo instante.
3. Halle, para cada instante, las componentes intrínsecas de la aceleración y el radio de curvatura en el mismo punto.

Todas las cantidades están expresadas en las unidades del SI.