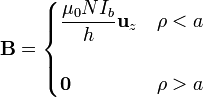Espira cuadrada en torno a solenoide

Revisión a fecha de 09:34 17 jun 2008; Antonio (Discusión | contribuciones)

Contenido

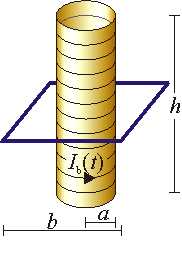
Una espira cuadrada de lado

b

, de resistencia

R

y autoinducción despreciable rodea concéntricamente a un solenoide circular largo, de radio

a

, de longitud

h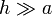

( $h\gg a$ ) y

N

espiras. Por el solenoide circula una corriente constante

I b 0

, que a partir de

t = 0

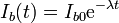
comienza a decaer exponencialmente como $I_b(t) = I_{b0} \mathrm{e}^{-\lambda t}\,$

Sabiendo que el campo magnético en el interior del solenoide es aproximadamente uniforme, calcule la corriente que circula por la espira cuadrada como función del tiempo.
Halle la carga que pasa por un punto de la espira durante todo el periodo $t > 0$ .
Halle la potencia instantánea disipada por efecto Joule en la espira, así como la energía total disipada en el periodo $t > 0$ .
Suponga ahora la misma situación descrita anteriormente, pero considere que la espira posee una autoinducción no despreciable $L$ y que inicialmente no circula corriente por ella. Para $t > 0$ la corriente que pasa por la espira es de la forma

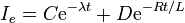
$I_e = C \mathrm{e}^{-\lambda t} + D \mathrm{e}^{-Rt/L}\,$

Calcule las constantes

C

y

D

, así como la carga que pasa por un punto de la espira en el periodo

t > 0

y la energía total disipada en el mismo periodo.

El campo magnético producido por un solenoide circular largo es

$\mathbf{B}=\begin{cases}\displaystyle\frac{\mu_0NI_b}{h}\mathbf{u}_z & \rho < a\\ & \\ \mathbf{0} & \rho > a\end{cases}$