5.2. Movimiento relativo en un sistema biela-manivela

De Laplace

Revisión a fecha de 21:22 22 nov 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Velocidades
3 Aceleraciones

1 Enunciado

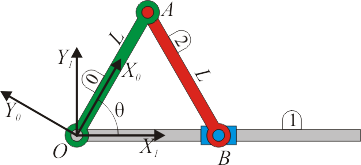
Se tiene un sistema biela-manivela formado por dos barras de longitud 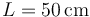$L=50\,\mathrm{cm}$ . La manivela (sólido “0”) gira alrededor de un punto O, extremo de una barra (sólido $1$ ) que podemos considerar fija. La biela (sólido “2”) está articulada a la manivela en un punto A, mientras que su otro extremo B está obligado a deslizar sobre la barra “1”.

En un instante dado la manivela forma con la barra un ángulo tal que $tg(θ) = 4 / 3$ . En el mismo instante las derivadas de este ángulo valen 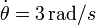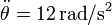$\dot{\theta}=3\,\mathrm{rad}/s$ , $\ddot{\theta}=12\,\mathrm{rad}/\mathrm{s}^2$ . Para este instante:

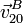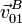Calcule las velocidades $\vec{v}^B_{21}$ , $\vec{v}^B_{20}$ y $\vec{v}^B_{01}$ . Indique su dirección y sentido gráficamente.
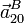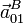Halle las aceleraciones $\vec{a}^B_{21}$ , $\vec{a}^B_{20}$ y $\vec{a}^B_{01}$ .

2 Velocidades

2.1 Absoluta

Desde el punto del vista del sólido 1, el punto B realiza un movimiento en una dimensión a lo largo de la barra.

La posición en cada instante corresponde a la base de un triángulo isósceles. Empleando una base ligada al sólido 1, según los ejes indicados en la figura

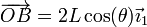
$\overrightarrow{OB}=2L\cos(\theta)\vec{\imath}_1$

Derivando esta posición respecto al tiempo obtenemos la velocidad absoluta del punto B

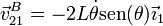
$\vec{v}^B_{21}=-2L\dot{\theta}\mathrm{sen}(\theta)\vec{\imath}_1$

Sustituyendo los valores numéricos tenemos, para las razones trigonométricas en el instante fijado,

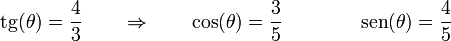
$\mathrm{tg}(\theta)=\frac{4}{3}\qquad\Rightarrow\qquad\cos(\theta)=\frac{3}{5}\qquad\qquad\mathrm{sen}(\theta)=\frac{4}{5}$

y de aquí

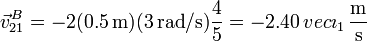
$\vec{v}^B_{21} = -2(0.5\,\mathrm{m})(3\,\mathrm{rad}/\mathrm{s})\frac{4}{5}=-2.40\,vec{\imath}_1\,\frac{\mathrm{m}}{\mathrm{s}}$

Esta velocidad puede también obtenerse como suma de la de arrastre más la relativa.

2.2 Relativa

2.3 Arrastre

La velocidad de arrastre, 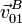$\vec{v}^B_{01}$ , es la que tendría el punto B si perteneciera al sólido 0, medida desde el sólido 1. El sólido 0 realiza una rotación pura en torno a un eje perpendicular al plano del sistema y que pasa por el punto de articulación

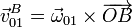
$\vec{v}^B_{01} = \vec{\omega}_{01}\times\overrightarrow{OB}$

La velocidad angular de este movimiento la da la variación del ángulo $θ$ con el tiempo

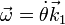
$\vec{\omega}=\dot{\theta}\vec{k}_1$

siendo la posición del punto B

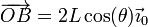
$\overrightarrow{OB}=2L\cos(\theta)\vec{\imath}_0$

lo que nos da la velocidad de arrastre

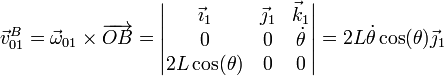
$\vec{v}^B_{01}=\vec{\omega}_{01}\times\overrightarrow{OB}=\left|\begin{matrix}\vec{\imath}_1 & \vec{\jmath}_1 & \vec{k}_1 \\ 0 & 0 & \dot{\theta}\\ 2L\cos(\theta) & 0 & 0\end{matrix}\right| = 2L\dot{\theta}\cos(\theta)\vec{\jmath}_1$

Sustituyendo los valores numéricos

$\vec{v}^B_{21}=2(0.50\,\mathrm{m})(3\,\mathrm{rad}/\mathrm{s})\frac{3}{5}\vec{\jmath}_0 = 1.8\vec{\jmath}_0\,\frac{\mathrm{m}}{\mathrm{s}}$

2.4 Representación gráfica

3 Aceleraciones

5.2. Movimiento relativo en un sistema biela-manivela

De Laplace

Contenido

1 Enunciado

2 Velocidades

2.1 Absoluta

2.2 Relativa

2.3 Arrastre

2.4 Representación gráfica

3 Aceleraciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES