5.2. Movimiento relativo en un sistema biela-manivela

De Laplace

Revisión a fecha de 20:29 22 nov 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Velocidades
- 2.1 Arrastre
3 Aceleraciones

1 Enunciado

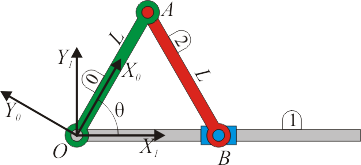
Se tiene un sistema biela-manivela formado por dos barras de longitud 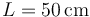$L=50\,\mathrm{cm}$ . La manivela (sólido “0”) gira alrededor de un punto O, extremo de una barra (sólido $1$ ) que podemos considerar fija. La biela (sólido “2”) está articulada a la manivela en un punto A, mientras que su otro extremo B está obligado a deslizar sobre la barra “1”.

En un instante dado la manivela forma con la barra un ángulo tal que $tg(θ) = 4 / 3$ . En el mismo instante las derivadas de este ángulo valen 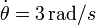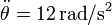$\dot{\theta}=3\,\mathrm{rad}/s$ , $\ddot{\theta}=12\,\mathrm{rad}/\mathrm{s}^2$ . Para este instante:

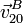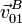Calcule las velocidades $\vec{v}^B_{21}$ , $\vec{v}^B_{20}$ y $\vec{v}^B_{01}$ . Indique su dirección y sentido gráficamente.
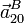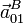Halle las aceleraciones $\vec{a}^B_{21}$ , $\vec{a}^B_{20}$ y $\vec{a}^B_{01}$ .