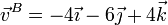4.4. Sólido en rotación instantánea
De Laplace
Revisión a fecha de 14:38 13 nov 2010; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 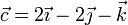 , de tal forma que la velocidad del punto B(0,2,1) es
, de tal forma que la velocidad del punto B(0,2,1) es
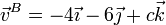
- Halle el valor de la constante c.
- Calcule la velocidad angular instantánea.
- Calcule la velocidad del punto C(1,1,0).
Todas las cantidades están expresadas en las unidades del SI.
2 Valor de la constante
Por ser A un punto del eje instantáneo de rotacion, EIR
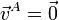
y la velocidad de cualquier otro punto, en particular B, verifica
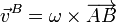
Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante
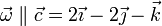

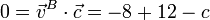

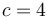
y resulta la velocidad para el punto B