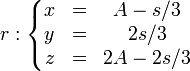No Boletín - Identificación de movimiento (Ex.Nov/10)

De Laplace

Revisión a fecha de 09:33 7 nov 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Trayectoria
3 Ley horaria
4 Identificación del movimiento

1 Enunciado

Una partícula se mueve según las ecuaciones horarias

$\vec{r}(t)=A\cos^2(\omega t)\vec{\imath}+2A\,\mathrm{sen}^2(\omega t)\vec{\jmath}+2A\cos^2(\omega t)\vec{k}$

¿Qué trayectoria sigue la partícula?
Determine la ley horaria $s (t)$ . Suponga que $s (0) = 0$ .
¿Qué tipo de movimiento describe la partícula?

2 Trayectoria

2.1 Método 1: Ecuaciones implícitas

La forma más directa de identificar la trayectoria consiste en buscar ecuaciones implícitas

$f(x,y,z) = 0\qquad\qquad g(x,y,z)=0$

que sean satisfechas por la posición instantánea en todo momento.

Separando en componentes tenemos que

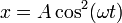
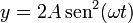
$x = A\cos^2(\omega t)\,$ $y=2A\,\mathrm{sen}^2(\omega t)$ $z=2A\cos^2(\omega t)\,$

De aquí es inmediato que

$z= 2x\,$ $\Rightarrow$ $2x -z = 0\,$

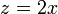
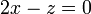
que es la ecuación de un plano, por lo que, por lo pronto, la trayectoria es plana.

Además, se verifica

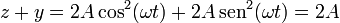
$z + y = 2A\cos^2(\omega t) + 2A\,\mathrm{sen}^2(\omega t) = 2A$

con lo que la trayectoria está también contenida en el plano

$z + y = 2A\,$

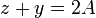
Al estar la trayectoria contenida en la intersección de dos planos, llegamos a la conclusión de que el movimiento es rectilíneo, siendo su trayectoria la recta

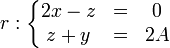
$r:\left\{\begin{matrix} 2x - z & = & 0 \\ z + y & = & 2A \end{matrix}\right.$

2.2 Método 2: Vector tangente

Un procedimiento sistemático para determinar un movimiento es rectilíneo consiste en determinar el vector tangente a la trayectoria y ver si éste es constante.

Hallamos este vector tangente calculando previamente la velocidad

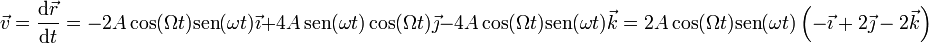
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-2A\cos(\Omega t)\mathrm{sen}(\omega t)\vec{\imath}+4A\,\mathrm{sen}(\omega t)\cos(\Omega t)\vec{\jmath}-4A\cos(\Omega t)\mathrm{sen}(\omega t)\vec{k}=2A\cos(\Omega t)\mathrm{sen}(\omega t)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)$

y dividiendo por su módulo, la celeridad,

$|\vec{v}| = 2A\cos(\Omega t)\mathrm{sen}(\omega t)\sqrt{1+4+4}=6A\cos(\Omega t)\mathrm{sen}(\omega t)$

lo que nos da el vector tangente

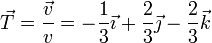
$\vec{T}=\frac{\vec{v}}{v}=-\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{2}{3}\vec{k}$

Este vector es constante y por tanto el movimiento es rectilíneo. La ecuación de la recta la obtenemos a partir se la posición inicial y empleando este vector tangente como vector director

$\vec{r}(s) = \vec{r}_0 + s \vec{T} = A\vec{\imath}+2A\vec{k}*s\left(-\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{2}{3}\vec{k}\right)$

o, separando en componentes

$r:\left\{\begin{matrix} x & = & A - s/3 \\ y & = & 2s/3 \\ z & = & 2A -2s/3\end{matrix}\right.$

2.3 Método 3: Relaciones trigonométricas

3 Ley horaria

4 Identificación del movimiento

No Boletín - Identificación de movimiento (Ex.Nov/10)

De Laplace

Contenido

1 Enunciado

2 Trayectoria

2.1 Método 1: Ecuaciones implícitas

2.2 Método 2: Vector tangente

2.3 Método 3: Relaciones trigonométricas

3 Ley horaria

4 Identificación del movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES