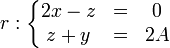No Boletín - Identificación de movimiento (Ex.Nov/10)

De Laplace

1 Enunciado

Una partícula se mueve según las ecuaciones horarias

1. ¿Qué trayectoria sigue la partícula?
2. Determine la ley horaria s(t). Suponga que s(0) = 0.
3. ¿Qué tipo de movimiento describe la partícula?

2 Trayectoria

2.1 Método 1: Ecuaciones implícitas

La forma más directa de identificar la trayectoria consiste en buscar ecuaciones implícitas

que sean satisfechas por la posición instantánea en todo momento.

Separando en componentes tenemos que

                

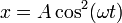
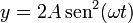
De aquí es inmediato que

      

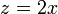
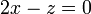
que es la ecuación de un plano, por lo que, por lo pronto, la trayectoria es plana.

Además, se verifica

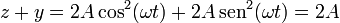
con lo que la trayectoria está también contenida en el plano

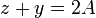
Al estar la trayectoria contenida en la intersección de dos planos, llegamos a la conclusión de que el movimiento es rectilíneo, siendo su trayectoria la recta

2.2 Método 2: Vector tangente

2.3 Método 3: Relaciones trigonométricas

3 Ley horaria

4 Identificación del movimiento